CBSE 12TH MATHEMATICS - Online Test
Q1. Derivative of cos (sin x) w.r.t. sin x is
Answer : Option D
Explaination / Solution:
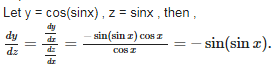
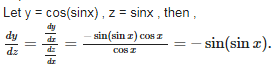
Q2. Find the coordinates of the foot of the perpendicular drawn from the origin to 2x + 3y + 4z – 12 = 0
Answer : Option D
Explaination / Solution:
D.R.’s of the line are < 2 , 3 , 4 > .
Therefore , equation of the line is :
Thus , the coordinates of any point P on the above line are P ( 2 , 3 ,4 ) .
But , this point P also lies on the given plane:
2(2) + 3(3 ) +4(4) – 12 = 0.
Therefore , the coordinates of the foot of perpendicular are given by :
Therefore , equation of the line is :
Thus , the coordinates of any point P on the above line are P ( 2 , 3 ,4 ) .
But , this point P also lies on the given plane:
2(2) + 3(3 ) +4(4) – 12 = 0.
Therefore , the coordinates of the foot of perpendicular are given by :
Q3. Solution of is
Answer : Option D
Explaination / Solution:
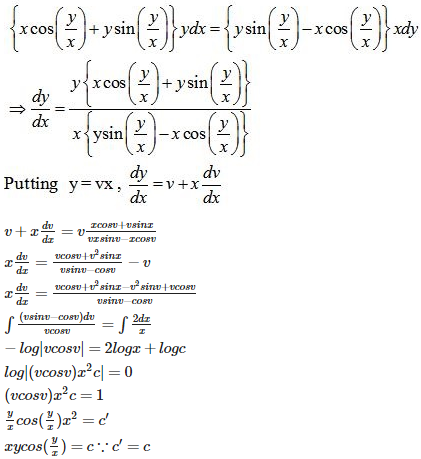
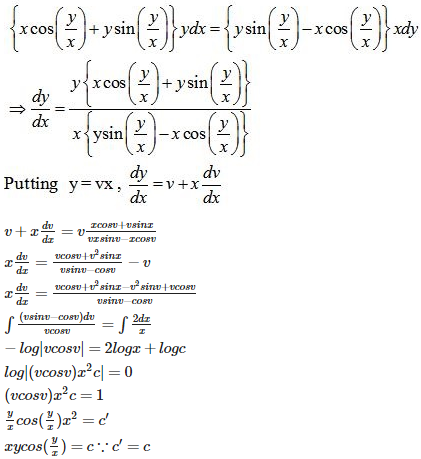
Q4. Find the approximate value of f(5.001) where
Answer : Option A
Explaination / Solution:
Q5.
Feasible region (shaded) for a LPP is shown in Figure. Maximize Z = 5x + 7y.
Answer : Option D
Explaination / Solution:
Corner points | Z = 5x +7 y |
O(0, 0 ) | 0
|
B (3,4) | 43…………………..(Max.) |
A(7,0 ) | 35 |
C(0,2) | 14 |
Hence the maximum value is 43
Q6. The range of function f(x) = [x] is :
Answer : Option D
Explaination / Solution:
integral part of x.
Q7. The value of det A where A=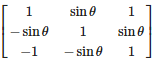 
lies in the interval
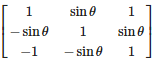lies in the interval
Answer : Option D
Explaination / Solution:
Q8. If , then x =
Answer : Option D
Explaination / Solution:
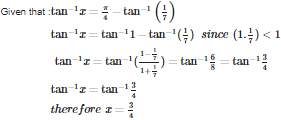
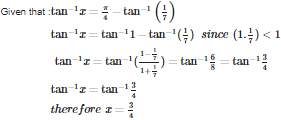
Q9. If A and B are square matrices of the same order and AB = 3 I, then is equal to
Answer : Option B
Explaination / Solution:
If A and B are square matrices of the same order and AB = 3 I, then ,
Q10. A differential equation of the form y' = F(x,y) is homogeneous if
Answer : Option C
Explaination / Solution:
A differential equation of the form y' = F(x,y) is homogeneous if F(x,y) is a homogeneous function of degree zero , so that we can convert it into variable separable form by y=vx.
