CBSE 12TH MATHEMATICS - Online Test
Q1. Find a unit vector perpendicular to each of 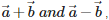 where
where 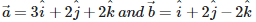
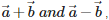 where
where 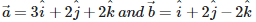
Answer : Option D
Explaination / Solution:
It is given that:

Therefore, the unit vector perpendicular to both the vectors
and
is given by:

Therefore, the unit vector perpendicular to both the vectors
and
is given by:
Q2. If then the value of the integral dx is equal to
Answer : Option D
Explaination / Solution:
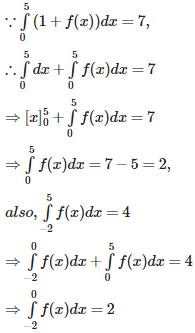
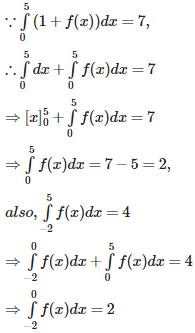
Q3. tan−114+tan−129=
Answer : Option D
Explaination / Solution:


Q4. The transformation ‘orthogonal projection on X-axis’ is given by the matrix
Answer : Option C
Explaination / Solution:
The orthogonal projection on x- axis is given by :
Q5. The differential coefficient of log (| log x |) w.r.t. log x is
Answer : Option C
Explaination / Solution:
Let y = then , we have ;
Q6. Find the distance of the point (2, 3, – 5) from the plane x + 2y – 2z = 9
Answer : Option C
Explaination / Solution:


Q7. At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (– 4, –3). Find the equation of the curve given that it passes through (–2, 1).
Answer : Option D
Explaination / Solution:
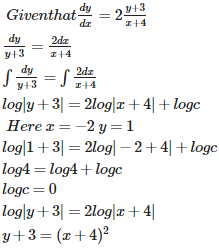
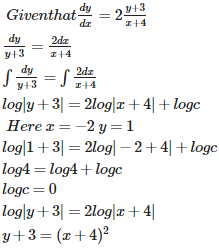
Q8. Let f (x) be differentiable in (0, 4) and f (2) = f (3) and S = {c : 2 < c < 3, f’ (c) = 0 } then
Answer : Option D
Explaination / Solution:
Since given f(x) is differentiable in (2,3) and f(2) = f(3) we have conditions of Rolle′s Theorem are satisfied by f(x) in [2,3]. Hence there exist atleast one real c in (2,3) s.t.f′
(c) = 0. Therefore, the set S contains atleast one element.
Q9. Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px+qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
Answer : Option D
Explaination / Solution:
We have Z = px + qy , At ( 3, 0 ) Z = 3p ……………………………….(1) At ( 1 , 1) Z = p + q …………………………(2) Therefore , from (1) and (2) : We have : p = q/2 .
Q10. The range of the function f(x) = [sin x] is
Answer : Option B
Explaination / Solution:
The only possible integral values of sin x are { -1 ,0, 1 }.As −1≤sinθ≤1
