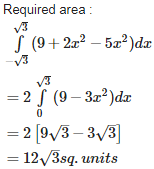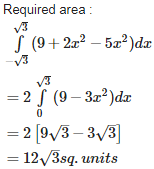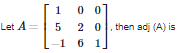CBSE 12TH MATHEMATICS - Online Test
Q1.
The number of solutions of the equation
Answer : Option C
Explaination / Solution:
As no value of x in ( 0, 1) can satisfy the given equation.Thus, the given equation has only one solution.
Q3. is equal to
Answer : Option A
Explaination / Solution:
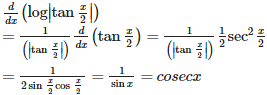
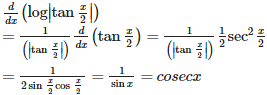
Q4. Find the distance of the point (3, – 2, 1) from the plane 2x – y + 2z + 3 = 0
Answer : Option B
Explaination / Solution:




Q5. Find the equation of a curve passing through the point (0, –2) given that at any point (x, y) on the curve, the product of the slope of its tangent and y coordinate of the point is equal to the x coordinate of the point.
Answer : Option B
Explaination / Solution:
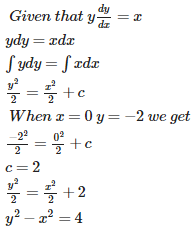
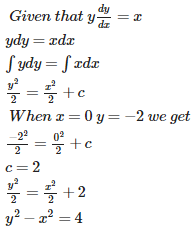
Q6. If a differentiable function f (x) has a relative minimum at x = 0, then the function y = f (x) + a x + b has a relative minimum at x = 0 for
Answer : Option B
Explaination / Solution:


Q7. Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5).Let F = 4x + 6y be the objective function. Maximum of F – Minimum of F =
Answer : Option A
Explaination / Solution:
Here the objective function is given by : F = 4x +6y .
Corner points | Z = 4x +6 y |
(0, 2 ) | 12………………..(Min.) |
(3,0) | 12………………….(Min.) |
(6,0 ) | 24 |
(6 , 8 ) | 72 |
(0 , 5 ) | 30 |
Maximum of F – Minimum of F = 72 – 12 = 30 .
Q8. The domain of definition of the function y=f(x)= √−x is :
Answer : Option A
Explaination / Solution:
y is defined if −x ⩾ 0 ,i.e.if x ⩽ 0, i.e. x ∈(−∞,0].
Q9. If A is a square matrix of order 2 , then det (adj A) =
Answer : Option C
Explaination / Solution:
Let A be a square matrix of order 2 then , because where n is the order of square matrix.
Q10. The area bounded by the parabolas y =
Answer : Option D
Explaination / Solution: