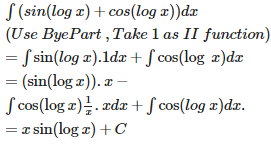CBSE 12TH MATHEMATICS - Online Test
Q1. The minimum value of f(x) =sin x cos x is
Answer : Option B
Explaination / Solution:


Q2. The domain of the function f = {(1,3), (3,5), (2,6)} is
Answer : Option B
Explaination / Solution:
The domain in ordered pair (x,y) is represented by x-co ordinate . Therefore, the domain of the given function is given by : { 1 , 3 , 2 }.
Q3. A(adj A) is equal to
Answer : Option C
Explaination / Solution:
Since, we know that
pre multiply by A,
(since AA-1=)
Q4.
The area bounded by the curves and the x- axis in the first quadrant is
Answer : Option A
Explaination / Solution:
To find area the curves y = and x = 2y + 3 and x – axis in the first quadrant., We have ;
,( y – 3 ) ( y + 1) = 0 . y = 3 , - 1 . In first quadrant , y = 3 and x = 9.
Therefore , required area is ;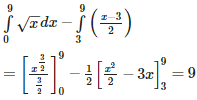
,( y – 3 ) ( y + 1) = 0 . y = 3 , - 1 . In first quadrant , y = 3 and x = 9.
Therefore , required area is ;
Q5. Find the unit vector in the direction of the vector 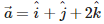
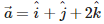
Answer : Option C
Explaination / Solution:
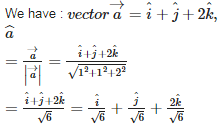
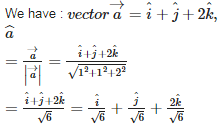
Q7. The number of solutions of the equation is
Answer : Option D
Explaination / Solution:

hence there is only one solution
Q8. Two matrices A and B are multiplicative inverse of each other only if
Answer : Option C
Explaination / Solution:
If AB = BA = I , then A and B are inverse of each other. i.e. A is invers of B and B is inverse of A.
Q9. is equal to
Answer : Option C
Explaination / Solution:
ddx(log|x|)=1|x|x|x|=x|x|2=xx2=1x
Q10. In the following case, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them. 2x – y + 3z – 1 = 0 and 2x – y + 3z + 3 = 0
Answer : Option B
Explaination / Solution:
We have ,
2x – y + 3z – 1 = 0 and 2x – y + 3z + 3 = 0 . Here ,
Therefore , the given planes are parallel.
2x – y + 3z – 1 = 0 and 2x – y + 3z + 3 = 0 . Here ,
Therefore , the given planes are parallel.