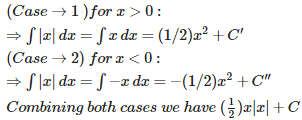CBSE 12TH MATHEMATICS - Online Test
Q1. Find the area of triangle with vertices ( 0 ,0 ),(4 , 2) and ( 1,1).
Answer : Option D
Explaination / Solution:


Q2. The area bounded by the curve y = 2x - and the line x + y = 0 is
Answer : Option D
Explaination / Solution:
The equation y = i.e.represents a downward parabola with vertex at ( 1, 1 ) which meets x – axis where y = 0 .i .e . where x = 0 , 2. Also , the line y = - x meets this parabola where – x = i.e. where x = 0 , 3.
Therefore , required area is :
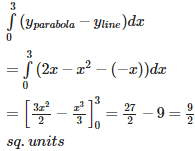
Therefore , required area is :
Q3. If is the angle between vectors then the cross product
Answer : Option D
Explaination / Solution:
If is the angle between vectors then, the cross product :
.
.
Q5. is equal to
Answer : Option A
Explaination / Solution:


Q6. The system of linear equations ax+ b y= 0, cx + dy = 0 has a non-trival solution if
Answer : Option A
Explaination / Solution:
The given system of equations has a non – trivial solution if :
Q7. If then is equal to
Answer : Option C
Explaination / Solution:


Q8. In the following case, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them. 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0
Answer : Option B
Explaination / Solution:
We have,
2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z = 0 . Here ,
Therefore , the given planes are parallel.
2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z = 0 . Here ,
Therefore , the given planes are parallel.
Q9. Differential equation of the family of parabolas having vertex at origin and axis along positive y-axis is
Answer : Option B
Explaination / Solution:
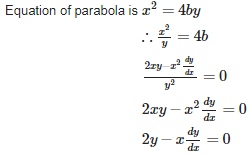
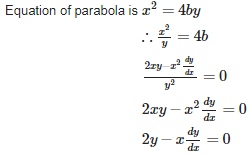
Q10. A farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
Answer : Option D
Explaination / Solution:
Let number of bags of cattle feed of brand P = x
And number of bags of cattle feed of brand Q = y
Therefore , the above L.P.P. is given as :
Minimise , Z = 250x +200y , subject to the constraints : 3 x + 1.5y ≥ 80, 2.5x + 11.25y ≥ 45, 2x + 3y ≥ 24 , x,y ≥ 0.,
Corner points | Z =250x +200 y |
C(0 , 12 ) | 2400
|
B (18,0) | 4500 |
D(3,6 ) | 1950…………………(Min.) |
A(9,2) | 2650 |
Here Z = 1950 is minimum.
i.e. 3 bags of brand P and 6 bags of brand Q; Minimum cost of the mixture = Rs 1950 .