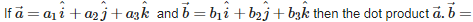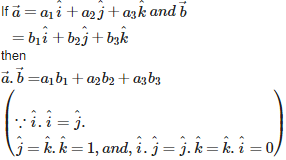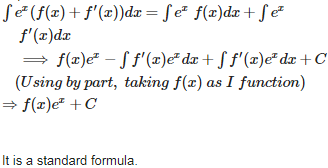CBSE 12TH MATHEMATICS - Online Test
Q3. If, then x =
Answer : Option A
Explaination / Solution:
Because , ,
Q4.
If A is square matrix such that , then is equal to
Answer : Option A
Explaination / Solution:
If A amd B are two square matrices of same order and the product AB= I, the matrix B is called inverse of matrix A.Therefore = I, then matrix A is the inverse of itself.
Q5. If , then is equal to
Answer : Option B
Explaination / Solution:
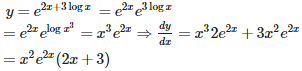
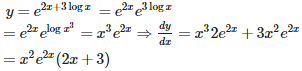
Q6. In the following case, determine whether the given planes are parallel orperpendicular, and in case they are neither, find the angles between them. 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
Answer : Option C
Explaination / Solution:
We have ,
2x + y + 3z – 2 = 0 and x – 2y + 5 = 0. Let
be the angle between the planes , then
As
Therefore , the given planes are perpendicular to each other.
2x + y + 3z – 2 = 0 and x – 2y + 5 = 0. Let
be the angle between the planes , then
As
Therefore , the given planes are perpendicular to each other.
Q7. Differential equation of the family of circles touching the y-axis at origin is
Answer : Option A
Explaination / Solution:
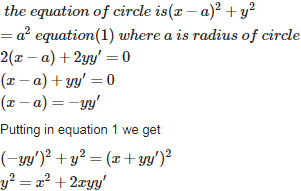
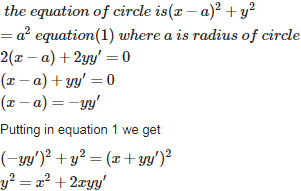
Q8. The corner points of the feasible region determined by the following system of linear inequalities:2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is
Answer : Option A
Explaination / Solution:
Here Z = px +qy , subject to constraints :
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0
As it is given that Z is maximum at ( 3 ,4 ) and ( 0, 5 ).
Therefore , 3p + 4q = 0p + 5q , which gives 3p = q .
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0
As it is given that Z is maximum at ( 3 ,4 ) and ( 0, 5 ).
Therefore , 3p + 4q = 0p + 5q , which gives 3p = q .
Q9. The function f (x) = has a
Answer : Option A
Explaination / Solution:
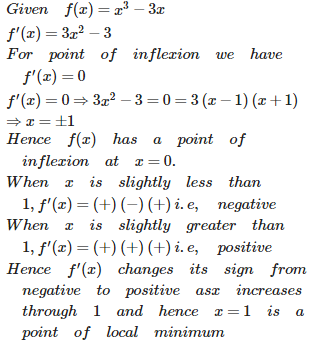
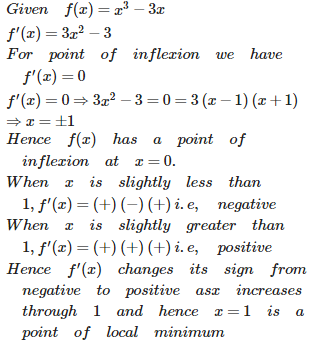
Q10. The diagram given below shows that


Answer : Option A
Explaination / Solution:
Because , an object in domain cann’t have two images in its co-domain.