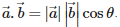CBSE 12TH MATHEMATICS - Online Test
Q1. If A and B are symmetric matrices of order n ( A≠ B), then
Answer : Option C
Explaination / Solution:
Sum of two symmetric matrices is also symmetric.
Q2. Find the angle between the planes whose vector equations are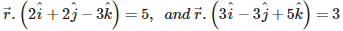 
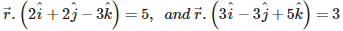
Answer : Option A
Explaination / Solution:
Q3.
Forming a differential equation representing the given family of curves by eliminating arbitrary constants a and b from yields the differential equation
Answer : Option C
Explaination / Solution:
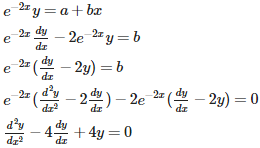
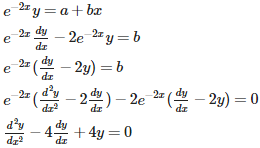
Q4. A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F1 costs Rs 4 per unit food and F2 costs Rs 6 per unit. One unit of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2 contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem. Find the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements.
Answer : Option B
Explaination / Solution:
Let number of units of food F1 = x
And number of units of food F2 = y
Therefore , the above L.P.P. is given as :
Minimise , Z = 4x +6y , subject to the constraints : 3 x + 6y ≥ 80, 4x + 3y ≥ 100, x,y ≥ 0.,
Corner points | Z =4x +6 y |
B(80/3 , 0 ) | 320/3 |
D(24,4/3 ) | 104…………………(Min.) |
A(0,100/3) | 200 |
Corner points Z =4x +6 y B(80/3 , 0 ) 320/3 D(24,4/3 ) 104…………………(Min.) A(0,100/3) 200 Here Z = 104 is minimum. i.e. Minimum cost = Rs 104.
Q5. The point on the curve where tangent makes an angle of with the X – axis is
Answer : Option A
Explaination / Solution:
Q6. The function f:R→R given by f(x)= cosx∀x∈R is :
Answer : Option C
Explaination / Solution:
f (0) = cos 0 = 1 ,and f (2π) =cos (2π)= 1. So , different elements in R may have the same image . Hence , f is not an injective function .Also, range of f(x) is not equal to its co-domain . So, f is not surjective.
Q8. The area bounded by the curve y =x, the x – axis and the ordinates x = 1 and x = -1 is given by
Answer : Option B
Explaination / Solution:
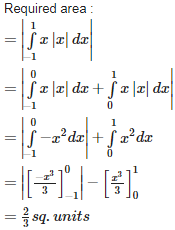
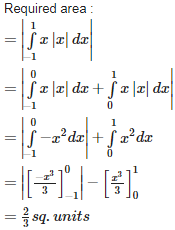
Q9. The scalar product of two nonzero vectors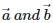 
is defined as
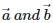is defined as
Answer : Option B
Explaination / Solution:
The scalar product of two nonzero vectors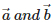 
is defined as :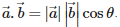 
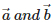is defined as : 
