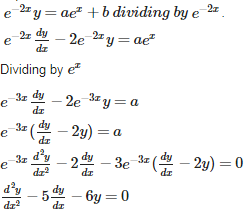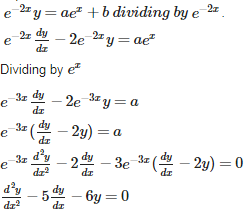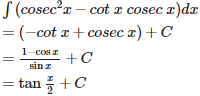cbse 12th mathematics | Online Objective Test

Application of Integrals Prepare / Learn

Q1. The area of bounded by the curve

\sqrt{x} + \sqrt{y} = 1

and the coordinate axes is

A. 1/2

B. 1/6

C. None of these

D. 1

Answer : Option B
Explaination / Solution:

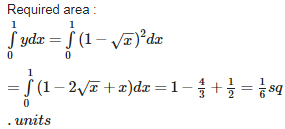
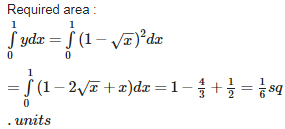
Relations and Functions Prepare / Learn

Q2. Let R be the relation in the set {1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}. Then R is

A. Symmetric and transitive but not reflexive.

B. Reflexive and symmetric but not transitive

C. An equivalence relation.

D. Reflexive and transitive but not symmetric

Answer : Option D
Explaination / Solution:

The relation R is not symmetric , (1,2) ∈R , but (2,1) ∉ R , (1,3) ∈R ,but (3,1) ∉ R , (3,2) ∈R, but (2,3) ∉R.

Determinants Prepare / Learn

Q3. A determinant is unaltered , if

A. Two rows are interchanged

B. Two columns are interchanged

C. To each element of any row is added the corresponding element of the other row multiplied by a given factor

D. Every element in a column is multiplied by the same factor

Answer : Option C
Explaination / Solution:

This is because of the elementary transformations of determinants . The value of determinant remains unaffected by applying elementary transformations.

Integrals Prepare / Learn

Q4.

$\int (1 - \cos x)$ $\cos e c^{2} x$ dx is equal to

A. 3cot2x3+C

B. cotx2+C

C. tanx2+C

D. 12tanx+C

Answer : Option C
Explaination / Solution:

Vector Algebra Prepare / Learn

Q5. The scalar product of the vector

\hat{i} + \hat{j} + \hat{k}

with a unit vector along the sum of vectors

2 \hat{i} + 4 \hat{j} - 5 \hat{k} a n d λ \hat{i} + 2 \hat{j} + 3 \hat{k}

is equal to one. Find the value of

λ

A. λ = 1

B. λ = -1

C. λ = -2

D. λ = 2

Answer : Option A
Explaination / Solution:

Let

\vec{a} = \hat{i} + \hat{j} + \hat{k}, \vec{b} = 2 \hat{i} + 4 \hat{j} - 5 \hat{k}

and

\vec{c} = λ \hat{i} + 2 \hat{j} + 3 \hat{k},

Therefore, a unit vector along

\vec{b} + \vec{c}

is given by:

Also, scalar product of

\hat{i} + \hat{j} + \hat{k}

with above unit vector is 1.

Inverse Trigonometric Functions Prepare / Learn

Q6. Which of the following is different from

2 \tan^{- 1} x

A. sin−1(2x1−x2),|x|⩽1

B. None of these

C. cos−1(1−x21+x2),|x|⩾0

\tan^{- 1} (\frac{2 x}{1 - x^{2}}), | x | < 1

Answer : Option B
Explaination / Solution:

therefore , none of these is the right option.

Continuity and Differentiability Prepare / Learn

Q7.

\underset{x \to 0}{L t} (1 + 2 x)^{\frac{x + 3}{x}}

is equal to

A. none of these.

B. e3

C. e3/2

Answer : Option D
Explaination / Solution:

Matrices Prepare / Learn

Q8. If

A = [\begin{matrix} 0 & 2 & 3 \\ - 2 & 0 & - 7 \\ - 3 & 7 & 0 \end{matrix}]

, then ,which of the following is true :

A. A =- A’

B. A = - A

C. None of these.

D. A = A’

Answer : Option A
Explaination / Solution:

The given matrix is a skew – symmetric matrix.,therefore , A = - A’.

Three Dimensional Geometry Prepare / Learn

Q9. Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0.

A. x + z + 2 = 0

B. x + z + 5 = 0

C. – x – z + 2 = 0

D. x – z + 2 = 0

Answer : Option D
Explaination / Solution:

The equation of the plane through the line of intersection of the planes

Differential Equations Prepare / Learn

Q10. Forming a differential equation representing the given family of curves by eliminating arbitrary constants a and b from

y = a e^{3 x} + b e^{- 2 x}

yields the differential equation

A. y″ – y′– 6y = 0

B. y″ + y′– 6y = 0

C. y″ + y′+ 6y = 0

D. y″ – y′+ 6y = 0

Answer : Option A
Explaination / Solution:

CBSE 12TH MATHEMATICS - Online Test

Prepare Before Start Test | Learn

UPSC Civil services Entrance exams | Online Test

GATE Exam | Online Test

Under Graduate Entrance Exams | Online Test

Problem Solving and Reasoning | Online Test

CAT Entrance Exams | Online Test

CLAT LAW Entrance exams | Online Test

Banking Entrance exams | Online Test

UGC NET Entrance exams | Online Test

TANCET Anna University | Online Test

TN State Board | Online Test