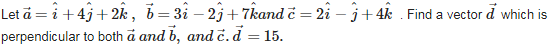CBSE 12TH MATHEMATICS - Online Test
Q1. If 1/a+1/b+ 1/c = 0 , then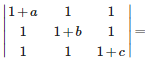 
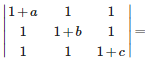
Answer : Option C
Explaination / Solution:
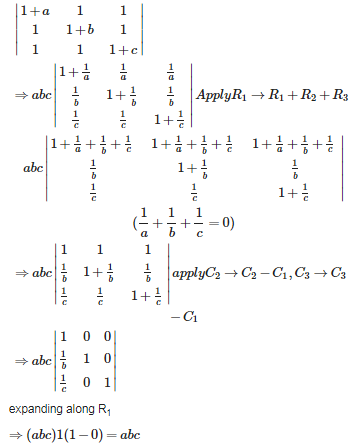
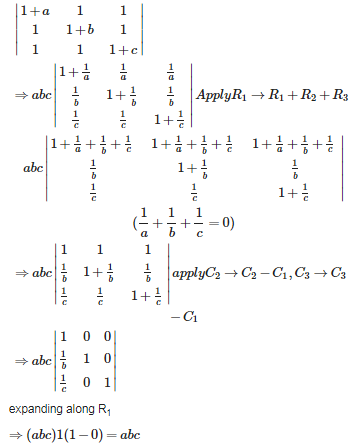
Q2. Which of the following is not equal to
Answer : Option B
Explaination / Solution:
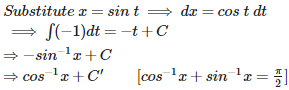
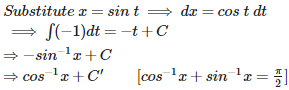
Q4. If then is equal to
Answer : Option A
Explaination / Solution:
tan−1x+tan−1(1x)tan−1x+cot−1x=π2
Q5. is equal to
Answer : Option D
Explaination / Solution:
Q6.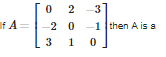 
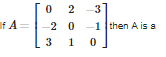
Answer : Option D
Explaination / Solution:
The diagonal elements of a skew – symmetric matrix is always zero and the elements aij= - aji
Q7. In vector form, if is the angle between the two planes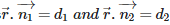 
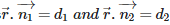then
then
Answer : Option B
Explaination / Solution:
In vector form, if is the angle between the two planes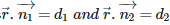 
then, cosine of the angle between these two lines is given by :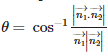 
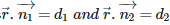then, cosine of the angle between these two lines is given by :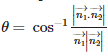
Q8.
Forming a differential equation representing the given family of curves by eliminating arbitrary constants a and b from yields the differential equation
Answer : Option A
Explaination / Solution:
2yy′=−2xyy′=−xyy′′+y′2+1=0
Q9. A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4hours for assembling. The profit is Rs 5 each for type A and Rs 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?
Answer : Option B
Explaination / Solution:
Let number of souvenirs of type A = x
And number of souvenirs of type B = y
Therefore , the above L.P.P. is given as :
Maximise , Z = 5x +6y , subject to the constraints : 5x +8y ≤ 200 and. 10x +8y ≤ 240 , x, y ≥ 0.
Corner points | Z =5x +6 y |
O( 0 , 0 ) | 0 |
D(0,25 ) | 150 |
A(24,0) | 120 |
B(8,20) | 160…………………(Max.) |
Here Z = 160 is maximum.
i.e. 8 Souvenir of types A and 20 of Souvenir of type B; Maximum profit = Rs 160.
Q10. The slope of the tangent to the curvex = a ( cos θ + θ sin θ),y = a (sin θ – θ cos θ) at any point ‘θ’ is
Answer : Option B
Explaination / Solution:
No Explaination.
