CBSE 12TH MATHEMATICS - Online Test
Q1. If f (x) = x then f ‘ (1 ) is equal to
Answer : Option B
Explaination / Solution:
Q2. Each diagonal element of a skew-symmetric matrix is
Answer : Option A
Explaination / Solution:
The diagonal elements of a skew-symmetric is zero.
Q3. Two lines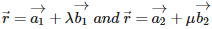 
are coplanar if
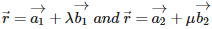are coplanar if
Answer : Option D
Explaination / Solution:
In vector form:
Two lines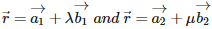 
are coplanar if (
.
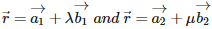are coplanar if (
Q4. To form a differential equation from a given function
Answer : Option A
Explaination / Solution:
We shall differentiate the function equal to the number of arbitrary constant so that we get equations equal to arbitrary constant and then eliminate them to form a differential equation
Q5. A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines tomanufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs 7 and screws B at a profit of Rs 10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximize his profit? Determine the maximum profit.
Answer : Option B
Explaination / Solution:
Let number of packages of screws A produced = x
And number of packages of screws B produced = y
Therefore , the above L.P.P. is given as :
Maximise , Z = 7x +10y , subject to the constraints : 4x +6y ≤ 240 and. 6x +3y ≤ 240 i.e. 2x +3y ≤ 120 and 2x +y ≤ 80 , x, y ≥ 0.
Corner points | Z =7 x +10 y |
O( 0 , 0 ) | 0 |
D(40,0 ) | 280 |
A(0,40) | 400 |
B(30,20) | 410…………………(Max.) |
Here Z = 410 is maximum.
i.e 30 packages of screws A and 20 packages of screws B; Maximum profit = Rs 410.
Q6. Equation of the tangent to the curve at the point (a, b) is
Answer : Option D
Explaination / Solution:
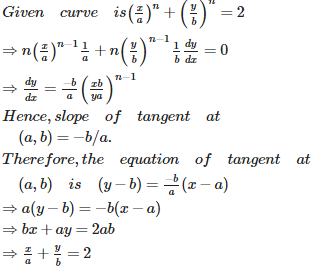
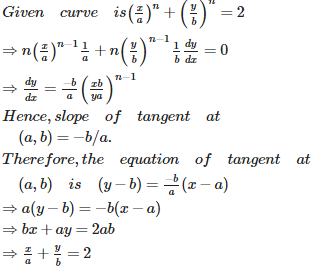
Q7. The area bounded by the curve and the line x + y = 3 is
Answer : Option B
Explaination / Solution:
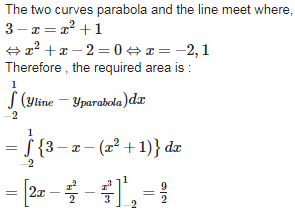
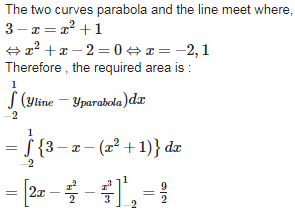
Q8. The relation R on the set Z of integers given by R = {(a, b): 2 divides a – b} ,∀ a, b ∈ Z is
Answer : Option C
Explaination / Solution:
- Since a – a = 0 , and 0 is divisible by 2 , therefore, aRa i.e. R is reflexive.
- If aRb , then a – b is divisible by 2. - ( a- b ) is divisible by 2. (b – a ) is divisible by 2. bRa i.e. R is symmetric. .
- .
- If aRb and bRc , then a – b is divisible by 2 and b – c is divisible by 2 a – b = 2q and b – c = 2q’ where q and q’ are integers. ( a – b ) + ( b – c ) = 2 ( q + q’) a – c =2( q + q’) ,,but (q +q’) is an integer. (a –c ) is divisible by 2. aRc i.e. R is transitive. .
Q9. The determinant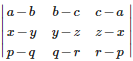 
is equal to
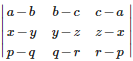is equal to
Answer : Option A
Explaination / Solution:
(Since C1 =0)
(Since C1 =0)
