CBSE 12TH MATHEMATICS - Online Test
Q1. Vector equation of a plane that passes through the intersection of planes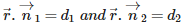 
expressed in terms of a non – zero constant is
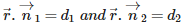expressed in terms of a non – zero constant is
Answer : Option C
Explaination / Solution:
Vector equation of a plane that passes through the intersection of planes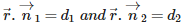 
expressed in terms of a non – zero constant is given by: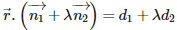 
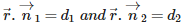expressed in terms of a non – zero constant is given by: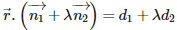
Q2. General solution of is
Answer : Option B
Explaination / Solution:
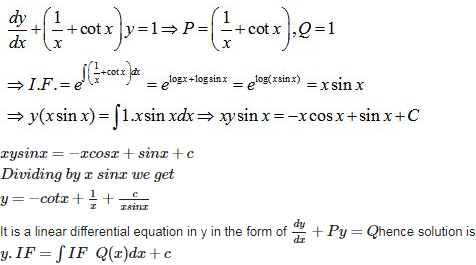
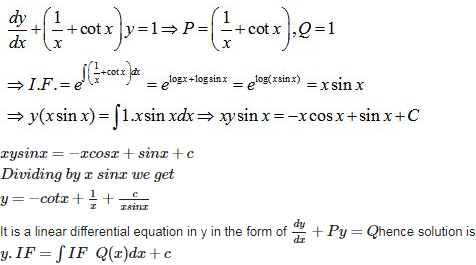
Q3. A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs17.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day?
Answer : Option B
Explaination / Solution:
Let number of packages of nuts produced = x
And number of packages of bolts produced = y
Therefore , the above L.P.P. is given as :
Maximise , Z = 17.50x +7y , subject to the constraints : x +3y ≤ 12 and. 3x +y ≤ 12, x, y ≥ 0.
Corner points | Z =17.50 x +7 y |
O( 0 , 0 ) | 0 |
D(4,0 ) | 70 |
A(0,4) | 28 |
B(3,3) | 73.50…………………(Max.) |
Here Z = 73.50 is maximum.
i.e 3 packages of nuts and 3 packages of bolts;
Maximum profit = Rs 73.50.
Q4.
Tangents to the curve at the points (1, 1) and ( – 1, 1)
Answer : Option D
Explaination / Solution:
therefore , slope of tangent at (1,1) = - 1 and the slope of tangent at ( - 1 ,1 )= 1 .
Now product of the slopes=1.-1= -1
Hence , the two tangents are at right angles.
Q5. The area bounded by the parabola and the line x + y = 3 is
Answer : Option B
Explaination / Solution:
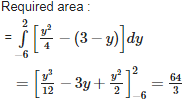
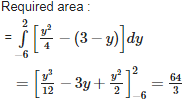
Q6. Let L be the set of all lines in a plane and R be the relation on L defined as R = {(L1, L2): L1 is perpendicular to L2}. Then R is
Answer : Option B
Explaination / Solution:
The relation R is symmetric only , because if L1 is perpendicular to L2 ,then L2 is also perpendicular to L1,but no other cases that is reflexive and transitive is not possible.
Q8. dx is equal to
Answer : Option C
Explaination / Solution:
∫log(1−x)dx−∫logx dx⇒(x−1)log(1−x)+1−xlnx+C
Q9. Find the value of x for which is a unit vector
Answer : Option D
Explaination / Solution:
As x is a unit vector ,
therefore,
therefore,
Q10. is equal to
Answer : Option C
Explaination / Solution:
