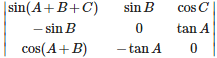CBSE 12TH MATHEMATICS - Online Test
Q1. if then tan θ is equal to
Answer : Option C
Explaination / Solution:


Q2. Differential coefficient of a function f (g (x)) w.r.t. the function g (x) is
Answer : Option C
Explaination / Solution:
dd(g(x))(f(g(x))=f′(g(x))
Q3. Adj.(KA) = ….
Answer : Option B
Explaination / Solution:
Adj.A , where K is a scalar and A is a n x n matrix.
Q4. Equation of a plane passing through three non collinear points (x1, y1, z1),(x2, y2, z2) and (x3, y3, z3) is
Answer : Option D
Explaination / Solution:
In cartesian co – ordinate system : Equation of a plane passing through three non collinear points (x1, y1, z1),(x2, y2, z2) and (x3, y3, z3) is given by : 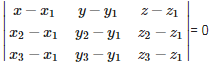
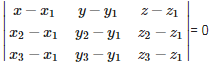
Q5. In a bank, principal increases continuously at the rate of r% per year. Find the value of r if Rs 100 double itself in 10 years (loge2 = 0.6931).
Answer : Option B
Explaination / Solution:
Let P be the principal at any time t. then,

When P = 100 and t = 0., then, c = 100, therefore, we have:
Now, let t = T, when P = 100., then;


When P = 100 and t = 0., then, c = 100, therefore, we have:
Now, let t = T, when P = 100., then;

Q6. One kind of cake requires 200g of flour and 25g of fat, and another kind of cake requires 100g of flour and 50g of fat. Find the maximum number of cakes which can be made from 5kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.
Answer : Option C
Explaination / Solution:
Let number of cakes of first type = x
And number of cakes of second type = y
Therefore , the above L.P.P. is given as :
Minimise , Z = x +y , subject to the constraints : 200x +100y ≤ 5000 and. 25x +50y ≤ 1000, i.e. 2x + y ≤ 50 and x +2y ≤ 40 x, y ≥ 0.
The corner points can be obtained by constructing the lines x+2y=40 , 2x+y= 50 and x+2y = 40.
The points so obtained are (0,0),(25,0), (20,10), and (0,20).
Corner points | Z = x + y |
O( 0 , 0 ) | 0 |
D(25,0 ) | 25 |
A(20,10) | 30……………..(Max.) |
B(0,20) | 20 |
Here Z = 30 is maximum.
i.e Maximum number of cakes = 30 , 20 of kind one and 10 cakes of another kind .
Q7. The slope of the tangent to the curve x = a sin t, y = a at the point ‘t’ is
Answer : Option D
Explaination / Solution:


Q8. The area included between the curves is equal to
Answer : Option A
Explaination / Solution:
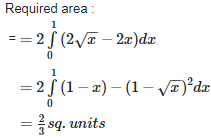
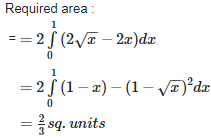
Q9. A relation R in a set A is called reflexive,
Answer : Option B
Explaination / Solution:
A relation R on a non empty set A is said to be reflexive if x Rx for all x ∈ R , Therefore , R is reflexive