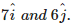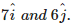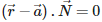CBSE 12TH MATHEMATICS - Online Test
Q2. The equation of a plane through a point whose position vector is and perpendicular to the vector . is
Answer : Option C
Explaination / Solution:
In vector form The equation of a plane through a point whose position vector is and perpendicular to the vector . Is given by :
Q3. Find the particular solution of the differential equation , given that y = 0 and x = 0.
Answer : Option D
Explaination / Solution:
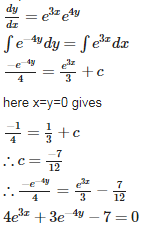
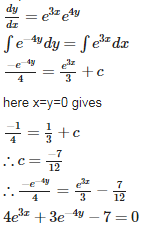
Q4. The curves cut orthogonally when
Answer : Option C
Explaination / Solution:
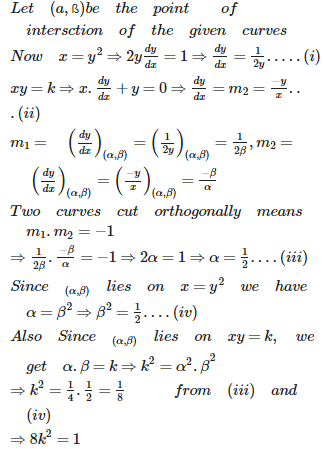
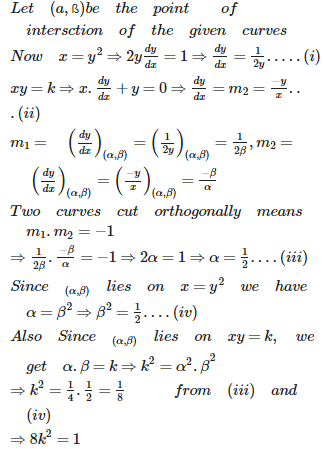
Q5. Maximize Z = – x + 2y, subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
Answer : Option C
Explaination / Solution:
Objective function is Z = - x + 2 y ……………………(1).
The given constraints are : x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
Corner points | Z = - x + 2y |
D(6,0 ) | -6 |
A(4,1) | -2 |
B(3,2) | 1 |
Here , the open half plane has points in common with the feasible region .
Therefore , Z has no maximum value.
Q6. The area bounded by the curves is equal to
Answer : Option A
Explaination / Solution:
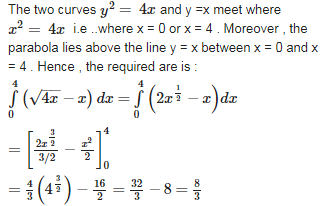
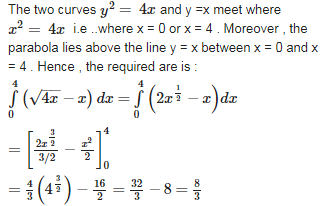
Q7. A relation R in a set A is called universal relation, if
Answer : Option B
Explaination / Solution:
The relation R = A x A is called Universal relation.
Q8. The roots of the equation det. 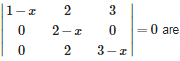
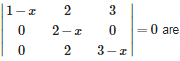
Answer : Option D
Explaination / Solution:
Expanding along C1


Q10. Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (– 5, 7).
Answer : Option C
Explaination / Solution:
The scalar and vector components of the vector with initial point (2, 1) and terminal point (– 5, 7) is given by : (- 5 – 2 ) i.e. – 7 and (7 – 1 ) i.e. 6. Therefore, the scalar components are – 7 and 6 .,and vector components are -