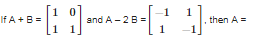CBSE 12TH MATHEMATICS - Online Test
Q1. Maximize Z = x + y, subject to x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0.
Answer : Option B
Explaination / Solution:
Objective function is Z = x + y ……………………(1).
The given constraints are : x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0.
Here , there is no common feasible region between the lines x – y = - 1 and - x + y = 0 .
Therefore , it has no solution. Thus , Z has no maximum value .
The given constraints are : x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0.
Here , there is no common feasible region between the lines x – y = - 1 and - x + y = 0 .
Therefore , it has no solution. Thus , Z has no maximum value .
Q2.
The area enclosed by the curve and the y – axis is
Answer : Option B
Explaination / Solution:
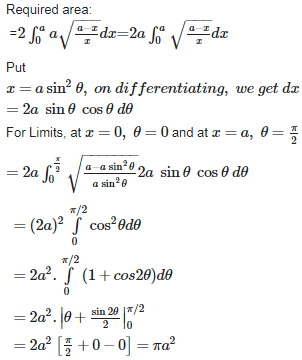
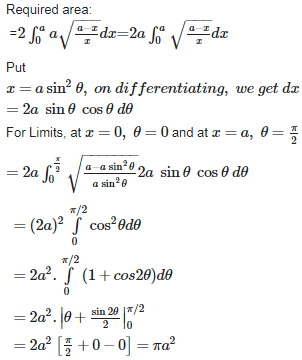
Q3. A Relation is a
Answer : Option D
Explaination / Solution:
By definition of Relation, : A relation from a non-empty set A to a non empty set B is a subset of A x B . If ( x, y) ∈ R , then we write xRy and we say that x is related to y through R.
Q4. One of the factors of 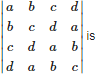
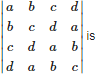
Answer : Option D
Explaination / Solution:


Therefore, one of the factors of given determinants is (a + b + c +d ).
Q5. If ∫ f(x) dx = f (x), then
Answer : Option B
Explaination / Solution:
It implies that the function remains same after integrating or differentiating it. So the function must be ex
Q6. Magnitude of the vector 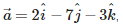 is
is
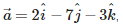 is
is
Answer : Option C
Explaination / Solution:
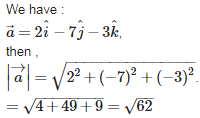
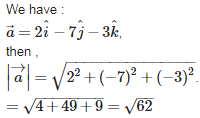
Q7. If = ,then x =
Answer : Option C
Explaination / Solution:
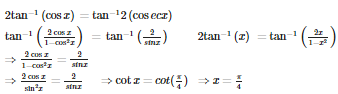
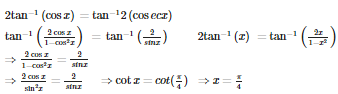
Q8. Let f be a function satisfying f(x + y) = f(x) + f(y) for all x, y then f ‘ (x) =
Answer : Option B
Explaination / Solution:
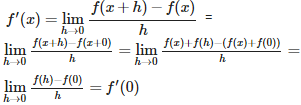
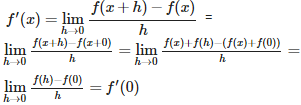
Q9. Equation of a plane which is at a distance d from the origin and the direction cosines of the normal to the plane are l, m, n is.
Answer : Option D
Explaination / Solution:
In Cartesian co – ordinate system Equation of a plane which is at a distance d from the origin and the direction cosines of the normal to the plane are l, m, n is given by : lx + my + nz = d.