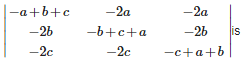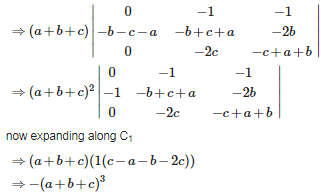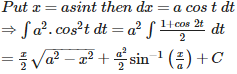CBSE 12TH MATHEMATICS - Online Test
Q1. Find the shortest distance between the lines : 



Answer : Option D
Explaination / Solution:
On comparing the given equations with:
, we get:

, we get:

Q2. From the matrix equation AB = AC we can conclude B = C, provided
Answer : Option D
Explaination / Solution:
Here , only non- singular matrices obey cancellation laws.
Q3. Find a particular solution of = 1; y =0 when x =2
Answer : Option A
Explaination / Solution:
Here y =0 when x =2
Hence
Q4. The normal to the curve x = a (cosθ+θsinθ),y = a (sinθ−θcosθ)at any point θ is such that
Answer : Option A
Explaination / Solution:
Equation of normal at θisxcosθ+ysinθ−a=0.So,normal is at a fixed distance a from the origin.
Q5. The area of the smaller portion of the circle cut off by the line x = 1 is
Answer : Option A
Explaination / Solution:
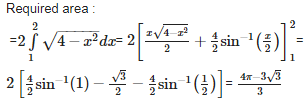
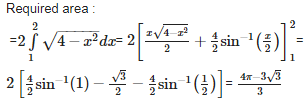
Q6. Minimize Z = 5x + 10 y subject to x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0
Answer : Option D
Explaination / Solution:
Objective function is Z = 5x + 10 y ……………………(1).
The given constraints are : x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0 .
The corner points are obtained by drawing the lines x+2y =120, x+y = 60 and x-2y = 0. The points so obtained are (60,30),(120,0), (60,0) and (40,20)
Corner points | Z = 5x + 10y |
D(60 ,30 ) | 600 |
A(120,0) | 600 |
B(60,0) | 300……………………..(Min.) |
C(40,20) | 400 |
Here , Z = 300 is minimum at ( 60, 0 ).
Q7. Let R = {(1, 3), (4, 2), (2, 4), (2, 3), (3, 1),(3,2)} be a relations on the set A = {1, 2, 3, 4}. The relation R is
Answer : Option C
Explaination / Solution:
R is said to be symmetric if (a,b)∈R⇒(b,a)∈R ,here (1,3)∈R⇒(3,1)∈R etc.
Q10. If two vectors have their corresponding direction cosines equal then the two vectors
Answer : Option B
Explaination / Solution:
If the direction cosines of two vectors are same , then the vectors are said to be parallel.