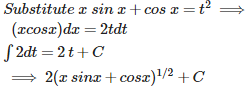CBSE 12TH MATHEMATICS - Online Test
Q1. The curve y = is inclined at to the X – axis at (0, 0) but it touches X – axis at (1, 0) , then the values of a, b, c, are given by
Answer : Option B
Explaination / Solution:
At ( 0 , 0) , slope of tangent = = 1. c = 1. At ( 1 ,0 ) , slope of tangent = 0.3a+2b+c=0. Also, when x = 1 , y = 0 , therefore , a + b + c = 0
At ( 0 , 0) , slope of tangent = = 1. c = 1. At ( 1 ,0 ) , slope of tangent = 0.3a+2b+c=0. Also, when x = 1 , y = 0 , therefore , a + b + c = 0
Q2.
The area between the hyperbola , then x – axis and the ordinates at a and b with a > b is :
Answer : Option C
Explaination / Solution:
Required area :
= = = =
= = = =
Q3. Minimize Z = x + 2y subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Answer : Option A
Explaination / Solution:
Objective function is Z = x + 2 y ……………………(1).
The given constraints are : 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0 .
Corner points | Z = x + 2y |
A(0 ,3 ) | 6…………………..(Minimum) |
B(6,0) | 6………………………(Minimum) |
Here , Z = 18 is minimum at ( 0, 3 ) and ( 6 , 0 ) .
Minimum Z = 6 at all the points on the line segment joining the points (6, 0) and (0, 3).
Q4. Given the relation R = {(1, 2), (2, 3)} on the set {1, 2, 3}, the minimum number of ordered pairs which when added to R make it an equivalence relation is =
Answer : Option B
Explaination / Solution:
To make the relation an equivalence relation , the following ordered pairs are required (1,1),(2,2),(3,3)(2,1)(3,2)(1,3),(3,1).
Q7. 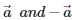 are
are
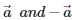 are
are
Answer : Option A
Explaination / Solution:
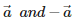 are collinear vectors , because they are parallel in direction and having the same magnitude.
are collinear vectors , because they are parallel in direction and having the same magnitude.
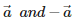 are collinear vectors , because they are parallel in direction and having the same magnitude.
are collinear vectors , because they are parallel in direction and having the same magnitude.
Q8. Evaluate P(A ∪ B), if 2P(A) = P(B) = and P(A|B) =
Answer : Option A
Explaination / Solution:
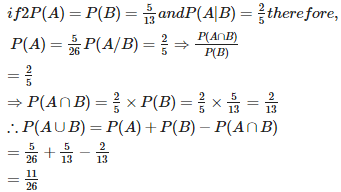
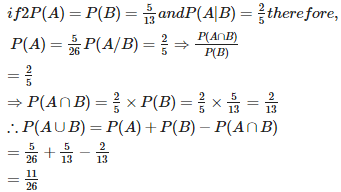
Q9. is equal to
Answer : Option B
Explaination / Solution:
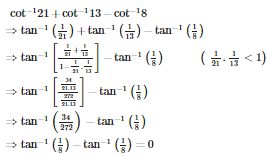
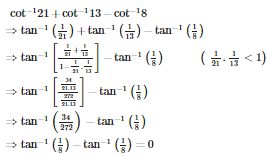
Q10. Let f(x) = x – [x], then f ‘ (x) = 1 for
Answer : Option B
Explaination / Solution:
f(x) = x - is derivable at all x R – I , and f ‘(x) = 1 for all x R – I
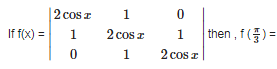
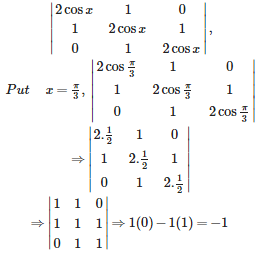
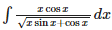 is equal to
is equal to