CBSE 12TH MATHEMATICS - Online Test
Q1. Let f(x) = | x−1|, then
Answer : Option A
Explaination / Solution:
here f(x)=|x−1| x∈R. So f(x) is not derivable when x−1=0 i.e. at x=1
Q2.
Find the values of p so that the linesare at right angles.
Answer : Option B
Explaination / Solution:


Q4. General solution of is
Answer : Option B
Explaination / Solution:
Since
Q5. The equation of the normal to the curve y = sinx at (0, 0) is
Answer : Option C
Explaination / Solution:
Since , therefore , slope of tangent at ( 0 , 0 ) = cos 0 = 1 and hence slope of normal at ( 0 , 0 ) is - 1 .
Q6. The area bounded by the parabola = x and the straight line 2y = x is
Answer : Option C
Explaination / Solution:
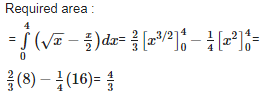
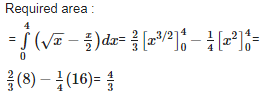
Q7. Maximise Z = 5x + 3y subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0.
Answer : Option A
Explaination / Solution:
Objective function is Z = 5x + 3 y ……………………(1).
The given constraints are : 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0.
The corner points obtained by drawing the lines 3x+5y=15 and 5x+2y=10 are (0,0),(0,3), (2,0) and (20/19,45/19)
Corner points | Z = 5x + 3 y |
O(0 , 0 ) | 0 |
B ( 2 , 0 ) | 10 |
C( 0 , 3 ) | 9 |
D ( 20/19 , 45/19 ) | 235/19 ……………….(Max.) |
Here , Z = 235/19 is maximum at ( 20/19 , 45/19 ) .
Q8. The binary operation * defined on the set of integers as a∗b=|a−b|−1is
Answer : Option D
Explaination / Solution:
Here * is commutative as b*a = |b−a|−1=|a−b|−1=a∗b.
Because ,|−x|=|x|for all x∈R.
Q9. Solution set of the equation 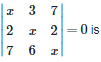
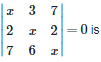
Answer : Option B
Explaination / Solution:


Q10. dx is equal to
Answer : Option A
Explaination / Solution:
∫cos((x−a)+a)cos(x−a)dx=∫cos(x−a)cosa−sin(x−a)sinacos(x−a)dx=∫{cosa−sinatan(x−a)}dx.xcosa+sinalog|cos(x–a)|+C
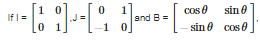 then B equals
then B equals
