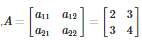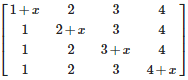cbse 12th mathematics | Online Objective Test

Inverse Trigonometric Functions Prepare / Learn

Q1. The value of the expression sinθ+cosθ lies between

A. 0 and 2 both inclusive.

B. -2 and 2 both inclusive

C. 0 and √2both inclusive

D. −√2 and √2 both inclusive

Answer : Option D
Explaination / Solution:

Minimum value =

(- \frac{1}{\sqrt{2}}) + (- \frac{1}{\sqrt{2}}) = - \sqrt{2}

and maximum value =

(\frac{1}{\sqrt{2}}) + (\frac{1}{\sqrt{2}}) = \sqrt{2}

Continuity and Differentiability Prepare / Learn

Q2. If both f and g are defined in a nhd of 0 ; f(0) = 0 = g(0) and f ‘ (0) = 8 = g’ (0), then

\underset{x \to 0}{L t} \frac{f (x)}{g (x)}

is equal to

A. 1

B. none of these

C. 0

D. 16

Answer : Option A
Explaination / Solution:

lim_{x \to 0} \frac{f (x)}{g (x)} = lim_{x \to 0} \frac{f^{'} (x)}{g^{'} (x)} = \frac{f^{'} (0)}{g^{'} (0)} = 1

( by using L’Hospital Rule )

Three Dimensional Geometry Prepare / Learn

Q3. Find the equation of the line in cartesian form that passes through the point (– 2, 4, – 5) and parallel to the line given by

\frac{x + 3}{3} = \frac{y - 4}{5} = \frac{z + 8}{6}

A. x+53=y−45=z+56

B. x+43=y−45=z+56

C. x+33=y−45=z+56

D. x+33=y−45=z+56

Answer : Option D
Explaination / Solution:

Find the equation of the line in cartesian form that passes through the point (– 2, 4, – 5) and parallel to the line given by

\frac{x + 3}{3} = \frac{y - 4}{5} = \frac{z + 8}{6}

is given by:

\frac{x - x_{1}}{l} = \frac{y - y_{1}}{m} = \frac{z - z_{1}}{n}

x_{1} = - 2, x_{2} = 4, x_{3} = - 5

And l = 3 , m = 5 and n = 6 .
Therefore ,

\frac{x + 2}{3} = \frac{y - 4}{5} = \frac{z + 5}{6}

Differential Equations Prepare / Learn

Q4. General solution of

\frac{d y}{d x} + y = 1 (y \neq 1)

A. y = 1 + Ae−3x

B. y = 1 + Aex

C. y = 1 + Ae-x

D. y = B + Ae−x

Answer : Option C
Explaination / Solution:

\frac{d y}{d x} + y = 1 \frac{d y}{d x} + P y = Q H e r e P = 1, Q = 1 \Rightarrow I . F . = e^{\int P . d x} = e^{\int 1. d x} = e^{x} \Rightarrow y . e^{x} = \int 1. e^{x} . d x \Rightarrow y . e^{x} = e^{x} + A \Rightarrow y = 1 + A e^{- x}

It is of the form of linear differential equation.hence the solution is y X IF =

\int Q (x) * I F d x + c

Matrices Prepare / Learn

Q5. If

A = [a_{i j}]_{2 \times 2}

where

a_{i j} = i + j,

then A is equal to

Answer : Option A
Explaination / Solution:

If

A = [a_{i j}]_{2 \times 2}

where

a_{i j} = i + j,

then

A = [\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}] = [\begin{matrix} 2 & 3 \\ 3 & 4 \end{matrix}]

Application of Derivatives Prepare / Learn

Q6. The function f (x) = a x + b is strict increasing for all x∈Riff

A. a< 0

B. a = 0

C. a> 0

D. none of these

Answer : Option C
Explaination / Solution:

Since f ‘ (x ) = a , therefore , f ( x ) is strict increasing on R iff a >0

Application of Integrals Prepare / Learn

Q7. The area common to the circle

x^{2} + y^{2} = 16 a^{2}

and the parabola

y^{2}

= 6ax is

A. 4a23(8π+3–√)

B. none of these

C. 4a23(4π+3–√)

D. 4a23(4π−3–√)

Answer : Option C
Explaination / Solution:

Linear Programming Prepare / Learn

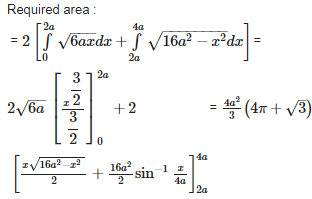
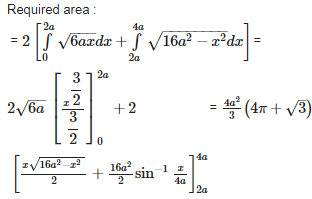
Q8. Maximise Z = 3x + 4y subject to the constraints: x + y ≤ 4, x ≥ 0, y ≥ 0.

A. Maximum Z = 16 at (0, 4)

B. Maximum Z = 19 at (1, 5)

C. Maximum Z = 17 at (0, 5)

D. Maximum Z = 18 at (1, 4)

Answer : Option A
Explaination / Solution:

Objective function is Z = 3x + 4 y ……(1).
The given constraints are : x + y ≤ 4, x ≥ 0, y ≥ 0.

The corner points obtained by constructing the line x+ y= 4, are (0,0),(0,4) and (4,0).

Corner points	Z = 3x +4y
O ( 0 ,0 )	Z = 3(0)+4(0) = 0
A ( 4 , 0 )	Z = 3(4) + 4 (0) = 12
B ( 0 , 4 )	Z = 3(0) + 4 ( 4) = 16 …( Max. )

therefore Z = 16 is maximum at ( 0 , 4 ) .

Relations and Functions Prepare / Learn

Q9. If A = { 1, 2, 3}, then the relation R = {(1, 2), (2, 3), (1, 3)} in A is

A. reflexive only

B. transitive only

C. symmetric only

D. symmetric and transitive only

Answer : Option B
Explaination / Solution:

A relation R on a non empty set A is said to be transitive if x Ry and y Rz ⇒xRz, for all x ∈ R. Here , (1, 2) and (2, 3) belongs to R implies that (1, 3) belongs to R.

CBSE 12TH MATHEMATICS - Online Test

Prepare Before Start Test | Learn

UPSC Civil services Entrance exams | Online Test

GATE Exam | Online Test

Under Graduate Entrance Exams | Online Test

Problem Solving and Reasoning | Online Test

CAT Entrance Exams | Online Test

CLAT LAW Entrance exams | Online Test

Banking Entrance exams | Online Test

UGC NET Entrance exams | Online Test

TANCET Anna University | Online Test

TN State Board | Online Test