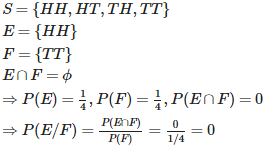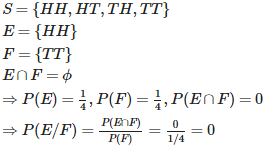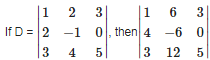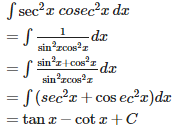CBSE 12TH MATHEMATICS - Online Test
Q1. General solution of ( -2 < y < 2) is
Answer : Option B
Explaination / Solution:
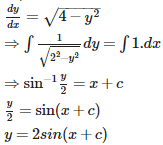
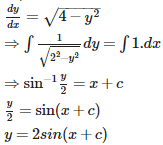
Q2. If, then for all natural numbers n, is equal to
Answer : Option D
Explaination / Solution:
Q3. Let g (x) be continuous in a neighbourhood of ‘a’ and g (a) ≠ 0. Let f be a function such that f ‘ (x) = g(x) then
Answer : Option A
Explaination / Solution:
Since g is continuous at a , therefore , if g ( a ) > 0 , then there is a neighbourhood of a, say ( a-e , a+ e ) in which g ( x ) is positive .This means that f ‘ (x)>0 in this nhd of a and hence f ( x ) is increasing at a.
Q4. The area bounded by the curves = x andy = is
Answer : Option A
Explaination / Solution:
The two curves meet in ( 0 , 0 ) and ( 1, 1 ).The required area lies above the curve y = x2 and below x = y2 and is equal to ;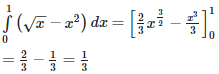
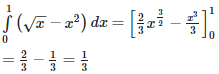
Q5. In linear programming problems the optimum solution
Answer : Option D
Explaination / Solution:
In linear programming problems the optimum solution satisfies a set of linear inequalities (called linear constraints) .
Q6. If A = { 1, 2, 3}, then the relation R = {(1, 2), (2, 3), (1, 3)} in A is
Answer : Option D
Explaination / Solution:
A relation R on a non empty set A is said to be transitive if xRy and y Rz⇒xRz, for all x ∈ R. Here , (1, 2) and (2, 3) belongs to R implies that (1, 3) belongs to R.
Q9. Unit vectors along the axes OX, OY and OZ are denoted by
Answer : Option D
Explaination / Solution:
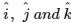represents the unit vectors along the co ordinate axes i.e. OX ,OY and OZ respectively.
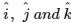represents the unit vectors along the co ordinate axes i.e. OX ,OY and OZ respectively.
Q10.
Two coins are tossed once ,where E :no tail appears , F : no head appers. Find P(E/F).
Answer : Option C
Explaination / Solution:
