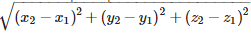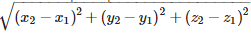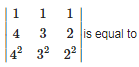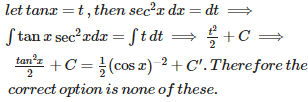CBSE 12TH MATHEMATICS - Online Test
Q1. Particular solution of a given differential equation
Answer : Option C
Explaination / Solution:
Particular solution of a given differential equation does not contain arbitrary constants i.e. a,b ,c etc since the value of those arbitrary can be found out by subsituting the given values.
Q2.
Shortest distance between the lines and is
Answer : Option B
Explaination / Solution:
Shortest distance between the lines and is given by: 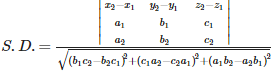
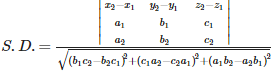
Q3. If A and B are any two matrices, then
Answer : Option C
Explaination / Solution:
Let matrix A is of order m x n , and matrix B is of order p x q . then , the product AB is defined only when n = p. that’s why, If A and B are any two matrices, thenAB may or may not be defined.
Q4. The area bounded by y = log x , the x – axis and the ordinates x = 1 and x = 2 is
Answer : Option C
Explaination / Solution:
Required area :
= = == = = =
= = == = = =
Q5. The optimal value of the objective function Z = ax + by may or may not exist, if the feasible region for a LPP is
Answer : Option A
Explaination / Solution:
The optimal value of the objective function Z = ax + by may or may not exist, if the feasible region for a LPP is unbounded. This is because the maximum or minimum value of the objective function may not exist.Even if it exists it must occur in a corner pointof the feasible region.
Q6.
Let and x, y R} be a relation in R. The relation R is
Answer : Option B
Explaination / Solution:
A relation R on a non empty set A is said to be symmetric if fx RyyRx, for all x , y R Clearly is same as for all x , y R. Therefore ,R is symmetric.
Q8. Let f (x) = then f (x) is
Answer : Option C
Explaination / Solution:
Hence an increasing function.
Q10. If and are any two points, then the vector joining P1 and P2 is the vector P1P2. Magnitude of the vector is
Answer : Option A
Explaination / Solution:
If and are any two points, then the vector joining P1 and P2 is the vector P1P2. then: =