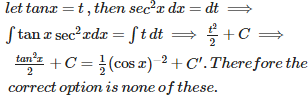CBSE 12TH MATHEMATICS - Online Test
Q1. Let f (x) = x – cos x, x∈R, then f is
Answer : Option D
Explaination / Solution:
Hence an increasing function.
Q2. The value of the determinant 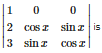
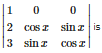
Answer : Option A
Explaination / Solution:
expanding along R1
Q3. In Corner point method for solving a linear programming problem one finds the feasible region of the linear programming problem ,determines its corner points and evaluates the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values at corner points. In case feasible region is unbounded, M is the maximum value of the objective function if
Answer : Option C
Explaination / Solution:
In Corner point method for solving a linear programming problem one finds the feasible region of the linear programming problem ,determines its corner points and evaluates the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values at corner points. In case feasible region is unbounded, M is the maximum value of the objective function if the open half plane determined by ax + by > M has no point in common with the feasible region . Otherwise Z has no maximum value.
Q4. Let A = {a, b, c} then the range of the relation R = {(a, b), (a, c), (b, c)} defined on A is
Answer : Option B
Explaination / Solution:
Since the range is represented by the y- co ordinate of the ordered pair ( x , y ).Therefore, range of the given relation is { b , c }.
Q6. If is a real number is a
Answer : Option C
Explaination / Solution:
If a vector is multiplied by any scalar then , the result is always a vector.
Q7. Two events A and B will be independent, if
Answer : Option D
Explaination / Solution:
Two events A and B will be independent, then
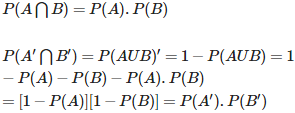
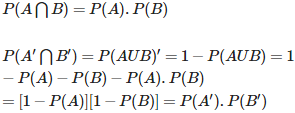
Q8. The general solution of the equation cotθ−tanθ=secθis(n∈I)
Answer : Option B
Explaination / Solution:
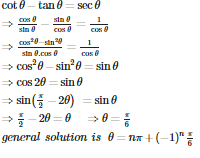
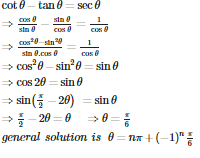
Q9. is
Answer : Option B
Explaination / Solution:
there fore answer is negative
there fore answer is negative
Q10. The function, f (x) = (x – a) sin for x a and f (a) = 0 is
Answer : Option D
Explaination / Solution: