CBSE 12TH MATHEMATICS - Online Test
Q1. Determine order and degree (if defined) ofcos() = 0
Answer : Option B
Explaination / Solution:
order = 2, degree not defined, because the function dy/dx present in angle of cosine function.
Q2.
Equation of a line through a point and having direction cosines l, m, n is
Answer : Option A
Explaination / Solution:
Equation of a line through a point (x1, y1, z1) and having direction cosines l, m, n is given by :
Q3. The area of the region between the curve y = 4 – and the x –axis is equal to
Answer : Option B
Explaination / Solution:
y = And
Required area:
= = =
Required area:
= = =
Q4. A square matrix A is called idempotent if
Answer : Option C
Explaination / Solution:
If the product of any square matrix with itself is the matrix itself , then the matrix is called Idempotent.
Q5.
The function f (x) = strictly increases on
Answer : Option A
Explaination / Solution:
Here ,
i.e. if x(x – 2 )<0 i.e. if 0 < x < 2. Hence f is strictly increasing on [0,2]
i.e. if x(x – 2 )<0 i.e. if 0 < x < 2. Hence f is strictly increasing on [0,2]
Q7. In Corner point method for solving a linear programming problem the second step after finding the feasible region of the linear programming problem and determining its corner points is
Answer : Option C
Explaination / Solution:
In Corner point method for solving a linear programming problem the second step after finding the feasible region of the linear programming problem and determining its corner points is : To evaluate the objective function Z = ax + by at each corner point.
Q8. If A is a finite set containing n distinct elements, then the number of relations on A is equal to
Answer : Option D
Explaination / Solution:
The number of elements in A x A is n x n = n2. hence ,the number of relations on A = number of subsets of A x A = 2nxn =.
Q9. The value of the integral dx lies in
Answer : Option B
Explaination / Solution:
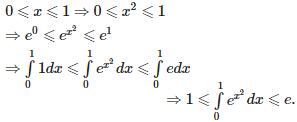
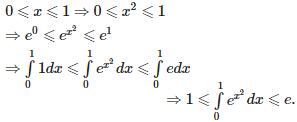
Q10. Vectors A and B are equal
Answer : Option B
Explaination / Solution:
Two vectors having same magnitude as well as same direction are always equal.