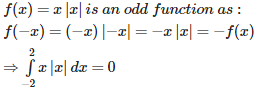CBSE 12TH MATHEMATICS - Online Test
Q1. If a matrix A is symmetric as well as skew symmetric then A is a
Answer : Option B
Explaination / Solution:
Only a null matrix can be symmetric as well as skew symmetric.
In Symmetric Matrix AT =A,
Skew Symmetric Matrix AT = -A,
Given that the matrix is satisfying both the properties therefore Equating the RHS we get A= -A i.e 2A=0 .
Therefore A=0,which is a null matrix.
Q2. Let f (x) = then f (x) is decreasing in
Answer : Option B
Explaination / Solution:
Here ,
Q3. If is non real cube root of unity , then 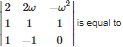
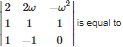
Answer : Option B
Explaination / Solution:
expanding along R3
Q4. In Corner point method for solving a linear programming problem the first step is to
Answer : Option D
Explaination / Solution:
In Corner point method for solving a linear programming problem the first step is : To find the feasible region of the linear programming problem and determine its corner points (vertices) either by inspection or by solving the two equations of the lines intersecting at that point.
Q5. Let A = {1, 2, 3}, then the relation R = {(1, 1), (1, 2), (2, 1)} on A is
Answer : Option C
Explaination / Solution:
A relation R on a non empty set A is said to be symmetric iff xRy⇔yRx, for all x , y ∈R Clearly , (1, 2), and (2, 1) both lies in R. Therefore ,R is symmetric.
Q7. Vectors A and B are Collinear
Answer : Option C
Explaination / Solution:
Two vectors A and B are said to be collinear , if they are parallel to the same line irrespective of their magnitudes and directions.
Q8. If E and F are independent, then
Answer : Option A
Explaination / Solution:
If E and F are independent, then P (E|F) = P (E), P (F) ≠ 0 .
Q9. is equal to
Answer : Option B
Explaination / Solution:
==
Q10. is equal to
Answer : Option B
Explaination / Solution:
( using L’Hospital Rule)