CBSE 11TH PHYSICS - Online Test
The moment of inertia of a solid sphere about a diameter is 8000 gms (mass of sphere = 50 gm, radius = 20 cm). The moment of inertia about a tangent will be
I = 2/5 MR2 = 8000 gm cm2 , using parallel axis theorem the moment of Inertia about tangent to sphere is = 2/5 MR2+ MR2 = 7/5 MR2. =2.8 gm cm2
A large steel wheel is to be fitted on to a shaft of the same material. At 27 C, the outer diameter of the shaft is 8.70 cm and the diameter of the central hole in the wheel is 8.69 cm. The shaft is cooled using ‘dry ice’. At what temperature of the shaft does the wheel slip on the shaft? Assume coefficient of linear expansion of the steel to be constant over the required temperature range: = 1.20 .
final temp. =
There are three rules on determining how many significant figures are in a number:
- Non-zero digits are always significant.
- Any zeros between two significant digits are significant.
- A final zero or trailing zeros in the decimal portion ONLY are significant.
So keeping these rules in mind, there are 4 significant digit.
Speed of the cyclist, v = 27 km/h = 7.5 m/s
Radius of the circular turn, r = 80 m
Centripetal acceleration is given as:
ac = 0.7 ms-2
The situation is shown in the given figure:
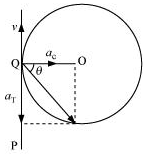
Suppose the cyclist begins cycling from point P and moves toward point Q. At point Q, he applies the breaks and decelerates the speed of the bicycle by 0.5 m/s2.
This acceleration is along the tangent at Q and opposite to the direction of motion of the cyclist.
Since the angle between ac and aT is 900, the resultant acceleration a is given by:
a =
= = 0.86 ms-2
tan θ =
where θ is the angle of the resultant with the direction of velocity.
tan θ = = 1.4
θ = tan-1(1.4) = 54.56° with the direction of velocity
