CBSE 11TH PHYSICS - Online Test

Answer : Option C
Explaination / Solution:

Moment of inertia of a disc about axis passing through Centre of mass and perpendicular to plane

Icm=12MR2

if I = Moment of inertia of a disc about axis passing through its edge and perpendicular to plane

applying parellal axis theorm

I=Icm+MR2I=12MR2+MR2I=32MR2

 

Answer : Option B
Explaination / Solution:
No Explaination.

Answer : Option C
Explaination / Solution:

E=32kT=32×1.38×10−23×10×106=2.07×10−16J

k = boltzman constant

Answer : Option D
Explaination / Solution:

A Kelvin degree and a Celsius degree means change in temperature.

Answer : Option B
Explaination / Solution:

Radius of cylinder r = 2 cm = 20 mm

Height of cylinder h = 10 cm = 100 mm

Surface area of cylinder = 2πr(r+h)

= 2×3.14×20(20+100)

= 2×3.14×20×120

= 15072 mm​​​​​2

 ≈1.5×104mm2

Answer : Option B
Explaination / Solution:

E=KE+PE

KE=12mω2A2sin2(ωt+ϕ)

PE=12mω2A2cos2(ωt+ϕ)

E=12mω2A2$E=\frac{1}{2}m{\omega }^2{A}^2$   (as) sin2(ωt+ϕ)+cos2(ωt+ϕ)=1

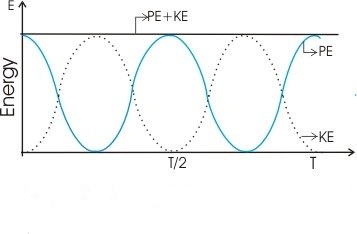
Thus total energy of the oscillator remains constant as displacement is regained after every half cycle.

 no energy is dissipated then all the potential energy becomes kinetic and vice versa.

Figure below shows the variation of kinetic energy and potential energy of harmonic oscillator with time where phase φ is set to zero for simplicity

Answer : Option B
Explaination / Solution:

The voltage in India is 220 volts, alternating at 50 cycles (Hertz) per second. This is the same as, or similar to, most countries in the world including Australia, Europe and the UK.

Answer : Option C
Explaination / Solution:
No Explaination.

Answer : Option D
Explaination / Solution:

Let L be the width of the film. Since the film has two surfaces, the total length along which the surface force acts on the slider is 2L. The surface tension S in the film is defined as the ratio of the surface force F to the length d (perpendicular to the force) along which the force acts

  S=F/d

Hence, in the case, d = 2L

S=F/2L

Answer : Option C
Explaination / Solution:

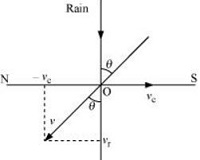
The described situation is shown in the given figure.

 Here,

vc = Velocity of the cyclist
vr = Velocity of falling rain

In order to protect herself from the rain, the woman must hold her umbrella in the direction of the relative velocity (v) of the rain with respect to the woman.
v = vr + (-vc)
= 30 + (-10) = 20 m/s
tan θ = vcvr=1030 
θ = tan-1 13