CBSE 11TH MATHEMATICS - Online Test
Q1. There are 10 true-false questions. The number of ways in which they can be answered is
Answer : Option A
Explaination / Solution:
you can either choose true or false, therefore for 10 questions you will have 210 possibilities.
Q2. The angle between the lines x = 1 , y = 2 and y = - 1 , z = 0 is
Answer : Option B
Explaination / Solution:
x = 1 , y = 2 represents XY plane and y = - 1 , z = 0 represents YZ plane.Since XY perpendicular to YZ .hence angle is 90 degrees
Q3. If k , l, m , n are four consecutive integers , then is equal to :
Answer : Option B
Explaination / Solution:
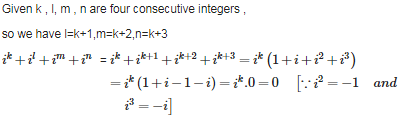
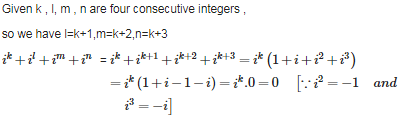
Q4. If A and B are two sets , then A∪(A∩B) is equal to
Answer : Option B
Explaination / Solution:
LetA={1,2,3,4}andB={1,2,3,4,5,6}HereA∩B={1,2,3,4}NowA∪(A∩B)={1,2,3,4,}=A
Q5. The coefficient of in the expansion of is
Answer : Option C
Explaination / Solution:
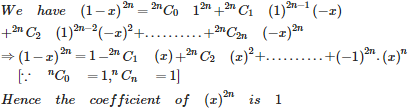
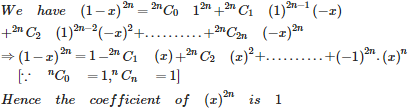
Q6. A solution is to be kept between and What is the range of temperature in degree Fahrenheit.What is the range of temperature in degree Fahrenheit if conversion formula is given by where C and F represent temperature in degree Celcius and degree Fahrenheit?
Answer : Option B
Explaination / Solution:
According to the question
Since , we get
Hence the range of temperature in degree Fahrenheit is between and
Q7. , where a > 0, is equal to
Answer : Option D
Explaination / Solution:
letx=1t;⇒Ltt→0at−1t=lna
Q8. If x, y, z are in A.P., then (x + 2y – z) (x + z – y) (z + 2y – x) is equal to
Answer : Option B
Explaination / Solution:
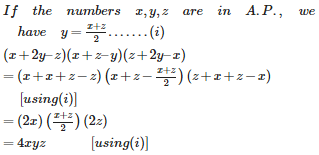
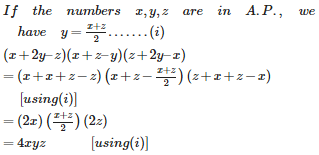
Q9. The coefficient of correlation r satisfies
Answer : Option D
Explaination / Solution:
r can't be numerically more than 1
Q10. The straight lines x + y - 4 = 0 , 3x + y – 4 = 0 , x - 3y – 4 = 0 form a triangle which is
Answer : Option A
Explaination / Solution:
The triangle formed by these lines is a right angled triangle
If the lines are perpendicular to each other, then the product of their slopes is -1
The slope of lines 3x + y – 4 = 0 , x - 3y – 4 = 0 are -3 and 1/3 respectively.
The product of the slopes is -1
Hence these two lines are perpendicular to each other
This infers that the triangle formed by these lines is a right angled triangle.
