CBSE 11TH MATHEMATICS - Online Test
Q1. The two consecutive terms in the expansion of , which have equal coefficients, are
Answer : Option A
Explaination / Solution:


Q2. The marks scored by Rohit in two tests were 65 and 70. Find the minimum marks he should score in the third test to have an average of atleast 65 marks.
Answer : Option D
Explaination / Solution:
Let x be the mark obtained by Rohit in the third test.
Then
Hence Rohit should get a minimum of 60 marks to get an average of atleast 65 marks.
Q3. If(x)=⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪sin[x][x]0,,[x]≠0,thenLtx→0f(x)[x]=0
Answer : Option A
Explaination / Solution:
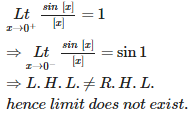
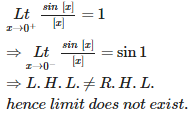
Q4. If the numbers a, b, c are in A.P., b, c, d are in G.P. and c, d , e are in H.P., then a, c, e are in
Answer : Option D
Explaination / Solution:


Q5. The statistical method which helps us to estimate or predict the unknown value of one variable from the known value of the related variable is called
Answer : Option B
Explaination / Solution:
It follows from the definition of regression
Q6. The equation of the line which passes through the point ( 2 , - 3 ) and cuts off equal intercepts from the axis is
Answer : Option C
Explaination / Solution:
The equation of the line which cuts equal intercepts is
x+y=a
Since it passes through (2,-3),
2 - 3 =a
Hence a = -1
Hence the equation of the required line is x + y +1 = 0
Q7. Which of the following is logically equivalent to (p∧q) ?
Answer : Option B
Explaination / Solution:
∼(∼(p∧q)) since∼p∨∼q≡∼(p∧q)
∼(∼p)≡p
Q8. The statement is true for all
Answer : Option C
Explaination / Solution:
when n = 1 , , which is not true.When n = 2, , which is false as well. Also when n = 3 we get .When n = 4 , Hence it is trure frm n = 4 .
Q9. The length of the common chord of the parabolas and is
Answer : Option D
Explaination / Solution:
point of intersection is (0,0) and (1,1). Hence by using the distance formula
=
Q10.
In a , Is equal to
Answer : Option D
Explaination / Solution:


