Control Systems - Online Test
Q1. Solution of the variables x1 and x2 for the following equations is to be obtained by
employing the Newton-Raphson iterative method.
equation (i) 10x2 sinx1 - 0.8 = 0
equation (ii) 10x2 - 10x2 cosx1 - 0.6 = 0
Assuming the initial valued x1 = 0.0 and x2 = 1.0, the jacobian matrix is
Answer : Option B
Explaination / Solution:
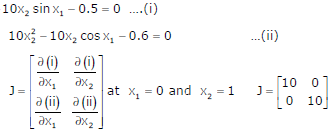
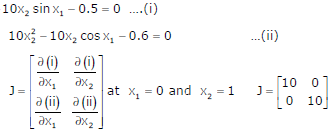
Q2.
An open loop system represented by the transfer function 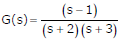 is
is
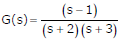 is
is
Answer : Option B
Explaination / Solution:
Open loop system stability is depends only on pole locations ⇒ system is stable
There is one zero on right half of s-plane so system is non – minimum phase
Q3. 
The frequency response of a linear system G(jw) is provided in the tubular form below

Answer : Option A
Explaination / Solution:
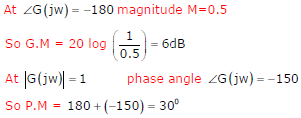
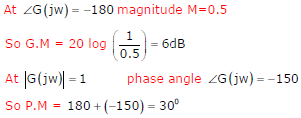
Q4. A point Z has been plotted in the complex plane, as shown in figure below.
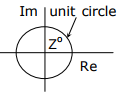

The plot of the complex number y = 1/z is
Answer : Option D
Explaination / Solution:
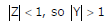
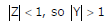
Z is having +ve real part and positive imaginary part (from the characteristics) So Y should have +ve real part and negative imaginary part.
Q5. 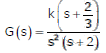
The open loop transfer function G(s) of a unity feedback control system is given as
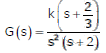
From the root locus, it can be inferred that when k tends to positive infinity,
Answer : Option A
Explaination / Solution:
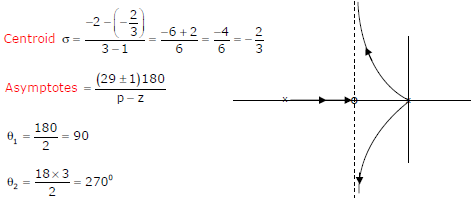
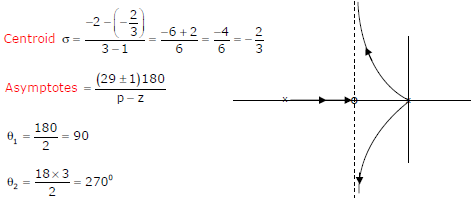
Q6. A two loop position control system is shown below
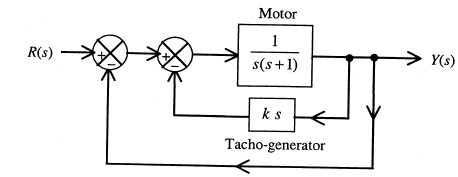

The gain k of the Tacho-generator influences mainly the
Answer : Option A
Explaination / Solution:
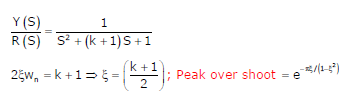
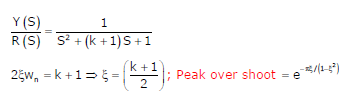
Q7. If 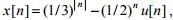 then the region of convergence (ROC) of its Z-transform in the
Z-plane will be
then the region of convergence (ROC) of its Z-transform in the
Z-plane will be
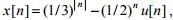 then the region of convergence (ROC) of its Z-transform in the
Z-plane will be
then the region of convergence (ROC) of its Z-transform in the
Z-plane will be
Answer : Option C
Explaination / Solution:
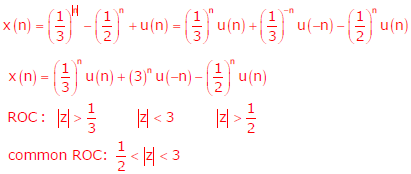
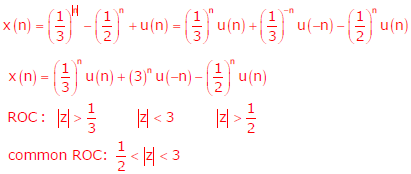
Q8. Given 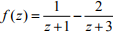 . If C is a counterclockwise path in the z-plane such that |z + 1| = 1, the value
of
. If C is a counterclockwise path in the z-plane such that |z + 1| = 1, the value
of 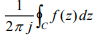 is
is
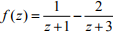 . If C is a counterclockwise path in the z-plane such that |z + 1| = 1, the value
of
. If C is a counterclockwise path in the z-plane such that |z + 1| = 1, the value
of 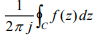 is
is
Answer : Option C
Explaination / Solution:
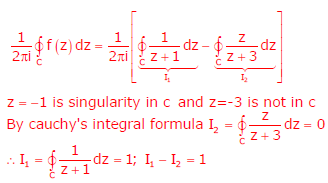
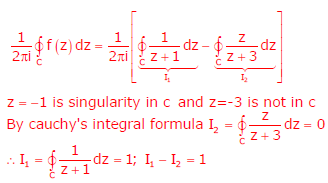
Q9. The unilateral Laplace transform of f (t) is 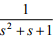 . The unilateral Laplace transform of
t f (t)
is
. The unilateral Laplace transform of
t f (t)
is
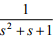 . The unilateral Laplace transform of
t f (t)
is
. The unilateral Laplace transform of
t f (t)
is
Answer : Option D
Explaination / Solution:
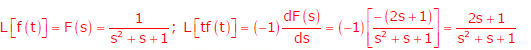
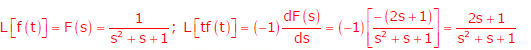
Q10. T he feedback system shown below oscillates at 2 rad/s when
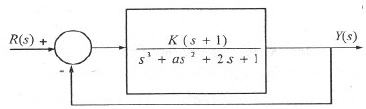
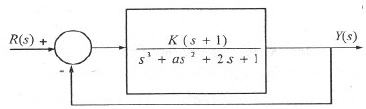
Answer : Option A
Explaination / Solution:


