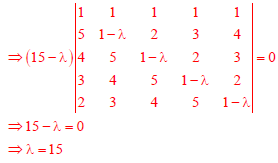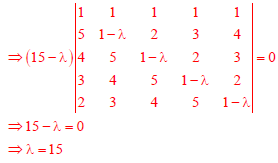Engineering Mathematics - Online Test
Q1. A fair coin is tossed 10 times. What is the probability that only the first two tosses will yield heads?
Answer : Option C
Explaination / Solution:
Number of elements in sample space is 210 Only one element "H,H,T,T,T,T,T,T,T,T, is event. Thus probability is 1/210
Q2.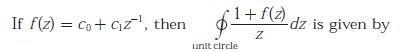 
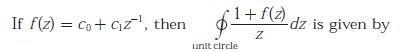
Answer : Option C
Explaination / Solution:
We have
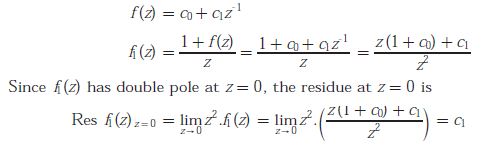
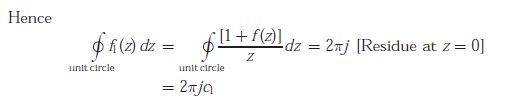
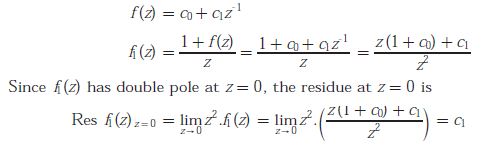
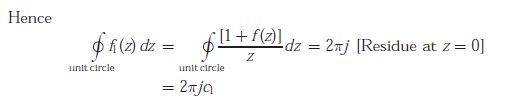
Q3. Consider the system
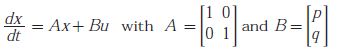
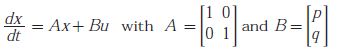
where p and q are arbitrary real numbers. Which of the following statements about the controllability of the system is true ?
Answer : Option C
Explaination / Solution:
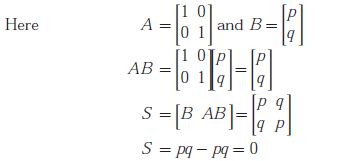
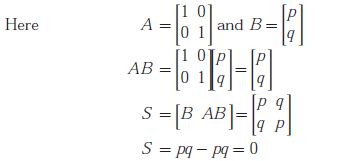
Since S is singular, system is completely uncontrollable for all values of p and q .
Q4. Consider two independent random variables X and Y with identical distributions. The variables X and Y take values 0, 1 and 2 with probabilities 1/2,1/4 and 1/4 respectively. What is the conditional probability P(X + Y = 2 X - Y = 0) ?
Answer : Option C
Explaination / Solution:
We have
Q5. The Taylor series expansion of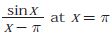 
is given by
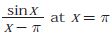is given by
Answer : Option D
Explaination / Solution:
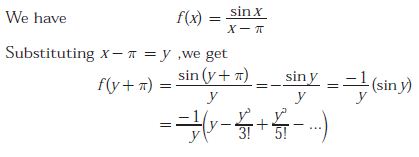
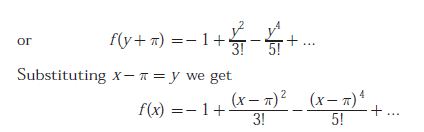
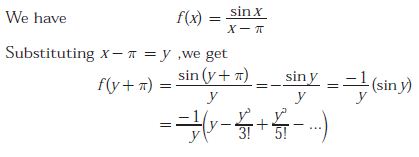
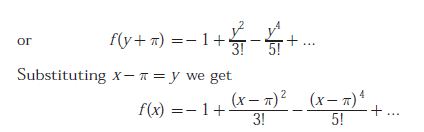
Q6. Given that F(s) is the one-side Laplace transform of f (t), the Laplace transform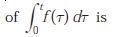 
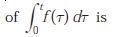
Answer : Option B
Explaination / Solution:
By property of unilateral laplace transform
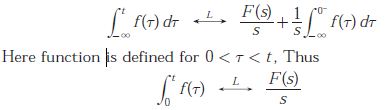
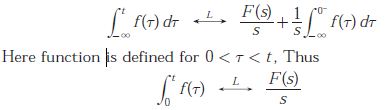
Q7. Match each differential equation in Group I to its family of solution curves from Group II
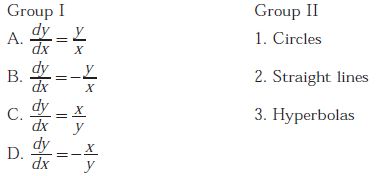
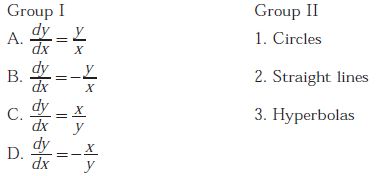
Answer : Option B
Explaination / Solution:
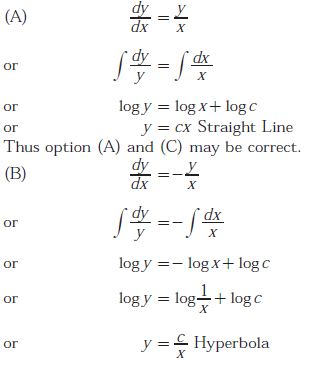
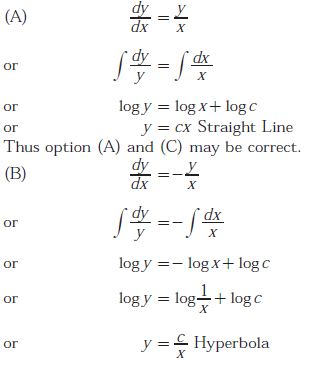
Q8. The Eigen values of following matrix are
Answer : Option D
Explaination / Solution:
Sum of the principal diagonal element of matrix is equal to the sum of Eigen values. Sum of the diagonal element is -1 - 1 + 3 = 1.In only option (D), the sum of Eigen values is 1.
Q9. Consider the following statement about the linear dependence of the real valued functions y1 =
1, y2 = x and y3 = x2, over the field of real numbers.
I. y1, y2 and y3 are linearly independent on -1 ≤ x ≤ 0
II. y1, y2 and y3 are linearly dependent on 0 ≤ x ≤ 1
III. y1, y2 and y3 are linearly independent on 0 ≤ x ≤ 1
IV. y1, y2 and y3 are linearly dependent on -1 ≤ x ≤ 0
Which one among the following is correct?
Answer : Option B
Explaination / Solution:
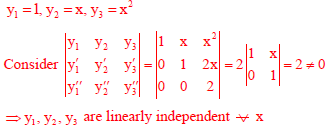
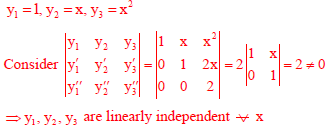
Q10. Consider the 5 × 5 matrix
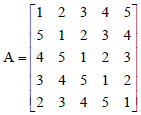
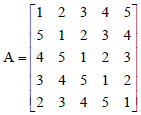
It is given that A has only one real eigen value. Then the real eigen value of A is
Answer : Option C
Explaination / Solution:
