Arithmetic - Online Test
Q1. There are 4 women P, Q, R, S, and 5 men V, W, X, Y, Z in a group. We are required to form
pairs each consisting of one woman and one man. P is not to be paired with Z, and Y must
necessarily be paired with someone. In how many ways can 4 such pairs be formed?
Answer : Option C
Explaination / Solution:
No Explaination.
Q2. In the graph below, the concentration of a particular pollutant in a lake is plotted over
(alternate) days of a month in winter (average temperature 10°C) and a month in summer
(average temperature 30°C).
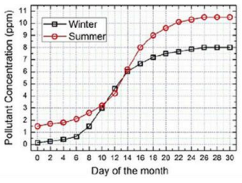
Consider the following statements based on the data shown above:
(i) Over the given months, the difference between the maximum and the minimum pollutant
concentrations is the same in both winter and summer.
(ii) There are at last four days in the summer month such that the pollutant concentrations on
those days are within 1 ppm of the pollutant concentrations on the corresponding days in
the winter month.
Which one of the following options is correct?
Answer : Option B
Explaination / Solution:
The difference between the maximum and the minimum pollutant concentrations
(i) in winter = 8-0=8 ppm ,
(ii) in summer = 10.5-1.5=9 ppm
(i) is false & (ii) is correct from the graph.
Q3. All people in a certain island are either 'Knights' or 'Knaves' and each person knows every
other person's identity. Knights NEVER lie, and knaves ALWAYS lie.
P says “Both of us are knights”. Q says “None of us are knaves”.
Which one of the following can be logically inferred from the above?
Answer : Option D
Explaination / Solution:
No Explaination.
Q4. X bullocks and Y tractors take 8 days to plough a field. If we halve the number of bullocks and
double the number of tractors, it takes 5days to plough the same field. How many days will it
take X bullocks alone to plough the field?
Answer : Option A
Explaination / Solution:
Given Number of days required that X bullocks and Y tractors to plough a field = 8 days ® (1) (i.e, X + Y ® 8D = 8X + 8Y ® 1dayNumber of days required that X/2 bullocks and 2y tractors to plough field = 5......(2)
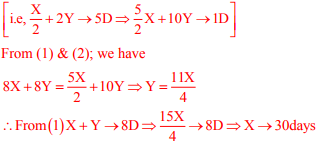
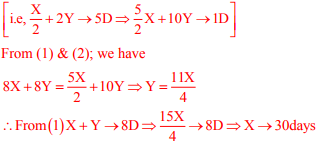
Q5. In a huge pile of apples and oranges, both ripe and unripe mixed
together, 15% are unripe fruits. Of the unripe fruits, 45% are apples.
Of the ripe ones, 66% are oranges. If the pile contains a total of
5692000 fruits, how many of them are apples?
Answer : Option A
Explaination / Solution:
Let T = total no of fruits = 5692000
R = Ripe fruits
U = Unripe fruits
A = Apple
O = Oranges
Given U = 15% of T : 15/100 × 5692000=853800
R = T – U= 4838200
A(U) = 45% of U: 45/100 × 853800 = 384210
A(R) = (100-66)% of R: 34/100 × 4838200 = 1644988
∴ A(U) + A(R) = 2029198
Q6. Michael lives 10 km away from where I live. Ahmed lives 5 km away
and Susan lives 7 km away from where I live. Arun is farther away
than Ahmed but closer than Susan from where I live. From the
information provided here, what is one possible distance (in km) at
which I live from Arun’s place?
Answer : Option C
Explaination / Solution:
In question it is given that Ahmed is 5Km away and Susan is 7Km
away from where I live. Further it is given that Arun is farther away
than Ahmed from where I live and not as far as Susan. That means
Arun must be living at distance more than 5Km but less than 7Km
from my house which is according to given options can be 6.02Km.
Note: Information about Michal is unnecessary and just given to
confuse.
Q7. A person moving through a tuberculosis prone zone has a 50%
probability of becoming infected. However, only 30% of infected
people develop the disease. What percentage of people moving
through a tuberculosis prone zone remains infected but does not
show symptoms of disease?
Answer : Option C
Explaination / Solution:
Percentage probability of being infected = P(A) = 50%
Percentage probability of infected person developing disease is having
system, = P(B) = 30%
∴ Percentage probability of infected person not showing symptoms =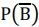 
= 70%
= 70%Percentage probability of person moving though a TB prone zone
remaining infected but not showing symptoms = P(A).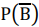
= 50/100 × 70/100 = 35%
= 50/100 × 70/100 = 35%
Q8. Leela is older than her cousin Pavithra. Pavithra’s brother Shiva is
older than Leela. When Pavithra and Shiva are visiting Leela, all three
like to play chess. Pavithra wins more often than Leela does. Which
one of the following statements must be TRUE based on the above?
Answer : Option D
Explaination / Solution:
According to given information the points we got are
a) Shiva is brother of Pavithra
b) Shiva and Pavithra are cousins of Leela
c) According to their ages Shiva > Leela > Pavithra
d) They all live play chess
e) Pavithra wins more often than Leela but information about
winning cases of Shiva is not given.
So from the given options statement which is clearly true is that
Pavithra is the youngest of all.
Q9. If q-a = 1/r and r-b = 1/s and S-c = 1/q, the value of abc is _______
Answer : Option C
Explaination / Solution:
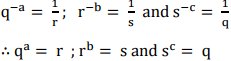
∴ a log q = log r -------(1)
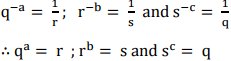
And b log r = log s ------(2)
And c log s = log q -----(3)
Multiplying equations (1), (2) and (3)
abc (log q) (log r)(log s) = (log r)(log s)(log q)
∴ abc = 1
Q10. P, Q, R and S are working on a project. Q can finish the task in
25 days, working alone for 12 hours a day. R can finish the task in 50
days, working alone for 12 hours per day. Q worked 12 hours a day
but took sick leave in the beginning for two days. R worked 18 hours
a day on all days. What is the ratio of work done by Q and R after 7
days from the start of the project?
Answer : Option C
Explaination / Solution:
After 7 days from start of project:
Q took sick leave on first 2 days
∴ Man hours by Q = 5×12
∴ Work done by Q = 5 × 12 × 1/(25×12) = 1/5
Man hours by R = 7×18
∴ Work done by R = 1/(50×12) × 7 × 18 = 21/100
∴ Ratio of work done by Q to work done by R = 1/5:21/100 = 100/(5×21) = 20/21
