REASONING - Online Test

Q1.

Directions:Questions in the form of inference/conclusions are based on the passages given below. Each passage is followed by five inferences. You are required to examine each inference separately in the context of the passage and decide upon its degree of truth or falsity.

Passage:

Many intellectuals didn’t appreciate the sheer profusion of unsolicited American gifts. Simone de Beauvoir complained about the use in hotels of noisy vacuum cleaners, preferring the humble French broom, and Sartre found his beloved existentialism upstaged by the real choices available to rootless and mobile Americans. However, anti-Americanism proved to be a losing game because so much of American influence was inseparable from the wider world project of modernization.

In a downbeat coda, Conrad concludes that our world has become “so Americanized that we no longer need to venerate the United States”. I am not sure that I wholly agree. To be sure, the past decades have provided many grounds for rejecting the vision of the future supplied by the US, and these days the American constitution looks less admirable than it did when Luce heralded the new century. No shortage of those prepared to say that America’s global sway is at an end can be discerned.

There has been such a widespread promulgation of American culture around the world that there is no more need to look up to the USA. Give answer –

A. if the inference is definitely true, i.e., it properly follows from the statement of facts given.

B. in the inference is probably true though not definitely true in the light of the facts given.

C. if the data are inadequate i.e., from the facts given you cannot say whether the inference is likely to be true or false.

D. if the inference is probably false though not definitely false in the light of the facts given.

E. if the inference is definitely false i.e., it cannot possibly be drawn from the facts given or it contradicts the given facts.

Answer : Option C
Explaination / Solution:

This is an opinion piece and the statement is one person's opinion being reported by the author of the piece. While the given statement might be true, there is no data to support the same

General mental ability Prepare / Learn

Q2.

Consider the following matrix:

3	370	7
2	224	6
1	730	X

What is the number at ‘X’ in the above matrix?

A. 5

B. 8

C. 9

D. 11

Answer : Option C
Explaination / Solution:
No Explaination.

Reasoning Ability Prepare / Learn

Q3. A CPU contains ____.

A. card-reader and a printing device

B. Analytical engine and a control unit

C. A control unit and an arithmetic logic unit

D. An arithmetic logic unit and a card reader

E. None of these

Answer : Option C
Explaination / Solution:

CPU has a number of components ,The first is the arithmetic logic unit (ALU), which performs simple arithmetic and logical operations. Second is the control unit (CU), which manages the various components of the computer.

Analytical Reasoning Prepare / Learn

Q4.

How many triangles and parallelograms are there in the following figure?

A. 21, 17

B. 19, 13

C. 21, 15

D. 19, 17

Answer : Option A
Explaination / Solution:

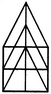
The figure may be labelled as shown.

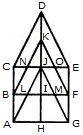
Triangles:

The simplest triangles are KJN, KJO, CNB, OEF, JIL, JIM, BLA and MFG i.e. 8 in number.

The triangles composed of two components each are CDJ, EDJ, NKO, JLM, JAH and JGH i.e. 6 in number.

The triangles composed of three components each are BKI, FKI, CJA and EJG i.e. 4 in number.

The triangles composed of four components each are CDE and AJG i.e. 2 in number.

The only triangle composed of six components is BKF.

Thus, there are 8 + 6 + 4 + 2 + 1 = 21 triangles in the given figure.

Parallelograms :

The simplest parallelograms are NJLB and JOFM i.e. 2 in number.

The parallelograms composed of two components each are CDKB, DEFK, BIHA and IFGH i.e.4 in number.

The parallelograms composed of three components each are BKJA, KFGJ, CJIB and JEFI i.e.4 in number.

There is only one parallelogram i.e. BFGA composed of four components.

The parallelograms composed of five components each are CDJA, DEGJ, CJHA and JEGH i.e.4 in number.

The only parallelogram composed of six components is CEFB.

The only parallelogram composed of ten components is CEGA.

Thus, there are 2 + 4 + 4 + 1 + 4+ 1 + 1 = 17 parallelograms in the given figure.

(Here note that the squares and rectangles are also counted amongst the parallelograms).

Logical Reasoning Prepare / Learn

Q5.

Passage:

Sartre felt that his ability to exercise power over his own actions was being threatened by the aids to decision making i.e. choices available to whimsical Americans. Give answer –

A. if the inference is definitely true, i.e., it properly follows from the statement of facts given.

B. in the inference is probably true though not definitely true in the light of the facts given.

C. if the data are inadequate i.e., from the facts given you cannot say whether the inference is likely to be true or false.

D. if the inference is probably false though not definitely false in the light of the facts given.

E. if the inference is definitely false i.e., it cannot possibly be drawn from the facts given or it contradicts the given facts.

Answer : Option A
Explaination / Solution:
No Explaination.

General mental ability Prepare / Learn

Q6. In a class of 45 students, a boy is ranked 20th. When two boys joined, his rank was dropped by one. What is his new rank from the end?

A. 25th

B. 26th

C. 27th

D. 28th

Answer : Option C
Explaination / Solution:
No Explaination.

Reasoning Ability Prepare / Learn

Q7. Computations and logical operations are performed by the -

A. RAM

B. ALU

C. Register

D. control unit

E. None of these

Answer : Option B
Explaination / Solution:
No Explaination.

Analytical Reasoning Prepare / Learn

Q8.

Count the number of squares in the given figure.

A. 22

B. 20

C. 18

D. 14

Answer : Option C
Explaination / Solution:

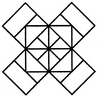
The figure may be labelled as shown.

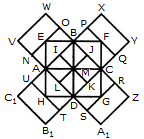
The squares composed of two components each are BJMI, CKMJ, DLMK and AIML i.e. 4 in number.

The squares composed of three components each are EBMA, BFCM, MCGD and AMDH i.e. 4 in number.

The squares composed of four components each are VWBA, XYCB, ZA₁DC and B₁C₁AD i.e. 4 in number.

The squares composed of seven components each are NOJL, PQKI, RSLJ and TUIK i.e. 4 in number.

There is only one square i.e. ABCD composed of eight components.

There is only one square i.e. EFGH composed of twelve components.

Total number of squares in the figure = 4 + 4 + 4 + 4 + 1 + 1 = 18.

Logical Reasoning Prepare / Learn

Q9.

Passage:

Modernization goes hand in hand with Americanization, in various degrees. Give answer –

A. in the inference is probably true though not definitely true in the light of the facts given.

B. if the data are inadequate i.e., from the facts given you cannot say whether the inference is likely to be true or false.

C. if the inference is definitely true, i.e., it properly follows from the statement of facts given.

D. if the inference is probably false though not definitely false in the light of the facts given.

E. if the inference is definitely false i.e., it cannot possibly be drawn from the facts given or it contradicts the given facts.

Answer : Option C
Explaination / Solution:
No Explaination.

General mental ability Prepare / Learn

Q10. In a rare coin collection, there is one gold coin for every three non-gold coins. 10 more gold coins are added to the collection and the ratio of gold coins to non-gold coins would be 1: 2. Based on the information, the total number of coins in the collection now becomes?

A. 90

B. 80

C. 60

D. 50

Answer : Option A
Explaination / Solution:
No Explaination.

REDO LAST TEST AGAIN : ( TEST 17 ) REDO THIS TEST AGAIN : ( TEST 18 )

START NEXT : ( TEST 19 )

reasoning TEST : 18