REASONING - Online Test
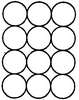
The figure may be labelled as shown.
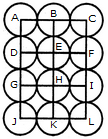
We shall join the centres of all the circles by horizontal and vertical lines and then label the resulting figure as shown.
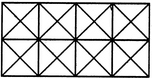
The simplest squares are ABED, BCFE, DEHG, EFIH, GHKJ and HILK i.e. 6 in number.
The squares composed of four simple squares are ACIG and DFLJ i.e. 2 in number.
Thus, 6 + 2 = 8 squares will be formed.
(B) Many developed countries are increasingly outsourcing IT related functions to India and China.
Count the number of triangles and squares in the given figure.
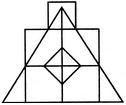
The figure may be labelled as shown.
Triangles :
The simplest triangles are BPN, PNE, ABM, EFG, MLK, GHI, QRO, RSO, STO and QTO i.e. 10 in number.
The triangles composed of two components each are BPE, TQR, QRS, RST and STQ i.e. 5 in number.
The triangles composed of three components each are MPO and GPO i.e. 2 in number.
The triangles composed of six components each are LPJ, HPJ and MPG i.e. 3 in number.
There is only one triangle LPH composed of twelve components.
Total number of triangles in the figure = 10 + 5 - 2 + 3 + 1 = 21.
Squares :
The squares composed of two components each are KJOM and JIGQ i.e. 2 in number.
The squares composed of three components each are ANOM, NFGO and CDEB i.e.3 in number.
There is only one square i.e. QRST composed of four components.
There is only one square i.e. AFIK composed of ten components.
Total number of squares in the figure = 2 + 3 + 1 + 1 = 7.
Expectation :
I. Health of at least some children would improve following this campaign.
II. Most of the parents would not buy video games for their children after this promotional campaign.
Consider that:
- A is taller than B.
- C is taller than A.
- D is taller than C.
- E is the tallest of all.
If they are made to sit in the above order of their height, who will occupy the mid position?
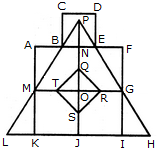
Count the number of squares in the given figure.
The figure may be labelled as shown.
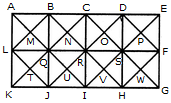
The squares composed of two components each are BNQM, CORN, DPSO, MQTL, NRUQ, OSVR, PFWS, QUJT, RVIU and SWHV i.e. 10 in number.
The squares composed of four components each are ABQL, BCRQ, CDSR, DEFS, LQJK, QRIJ, RSHI and SFGH i.e. 8 in number.
The squares composed of eight components each are BRJL, CSIQ and DFHR i.e. 3 in number.
The squares composed of sixteen components each are ACIK, BDHJ and CEGI i.e. 3 in number.
Thus, there are 10 + 8 + 3 + 3 = 24 squares in the figure.
