REASONING - Online Test

Count the number of triangles and squares in the given figure.
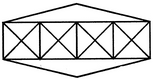
The figure may be labelled as shown.

Triangles:
The simplest triangles are BGM, GHM, HAM, ABM, GIN, UN, JHN, HGN, IKO, KLO, LJO, JIO, KDP, DEP, ELP, LKP, BCD and AFE i.e. 18 in number.
The triangles composed of two components each are ABG, BGH, GHA, HAB, HGI, GIJ, IJH, JHG, JIK, IKL, KLJ, LJI, LKD, KDE, DEL and ELK i.e. 16 in number.
The triangles composed of four components each are BHI, GJK, ILD, AGJ, HIL and JKE i.e. 6 in number.
Total number of triangles in the figure = 18 +16 + 6 = 40.
Squares :
The squares composed of two components each are MGNH, NIOJ and OKPL i.e. 3 in number.
The squares composed of four components each are BGHA, GIJH, IKLJ and KDEL i.e. 4 in number.
Total number of squares in the figure = 3 + 4 = 7.
Count the number of triangles and squares in the given figure.
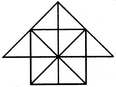
The figure may be labelled as shown.
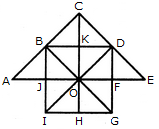
Triangles:
The simplest triangles are JBO, BKO, KDO, DFO, FGO, GHO, HIO, IJO, ABJ, BCK, CKD and DEF i.e.12 in number.
The triangles composed of two components each are IBO, BDO, DGO, GIO, ABO, CDO, CBO, CBD and DEO i.e. 9 in number.
The triangles composed of four components each are IBD, BDG, DGI, GIB, ACO and COE i.e. 6 in number.
There is only one. triangle i.e. ACE composed of eight components.
Thus, there are 12 + 9 + 6 + 1 = 28 triangles in the given figure.
Squares:
The squares composed of two components each are BKOJ, KDFO, OFGH and JOHI i.e. 4 in number.
There is only one square i.e. CDOB composed of four components.
There is only one square i.e. BDGI composed of eight components.
Thus, there are 4 + 1 + 1 = 6 squares in the given figure.
- All X-brand cars parked here are white.
- Some of them have radial types.
- All X-brand cars manufactured after 1986 have radial tyres.
- All cars are not X-brand.
Which one of the following conclusions can be drawn from the above statements?
What is the minimum number of different colours required to paint he given figure such that no two adjacent regions have the same colour?
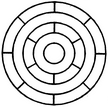
The figure may be labelled as shown.
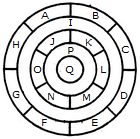
The regions A, C, E and G can have the same colour say colour 1.
The regions B, D, F and H can have the same colour (but different from colour 1) say colour 2.
The region 1 lies adjacent to each one of the regions A, B, C, D, E, F, G and H and therefore it should have a different colour say colour 3.
The regions J, L and N can have the same colour (different from colour 3) say colour 1.
The regions K, M and O can have the same colour (different fromthe colours 1 and 3). Thus, these regions will have colour 2.
The region P cannot have any of the colours 1 and 2 as it lies adjacent to each one of the regions J, K, L, M, N and O and so it will have colour 3.
The region Q can have any of the colours 1 or 2.
Minimum number of colours required is 3.
