GENERAL APTITUDE - Online Test
Q1. Direction: In the following number series, a wrong number is given. Find out that wrong number.
37, 54, 88, 142, 207, 292, 394
Answer : Option A
Explaination / Solution:
37 + 17 × 1 = 54
54 + 17 × 2 = 88
88 + 17 × 3 = 139
139+ 17 × 4 = 207
207 + 17 × 5 = 292
292+ 17 × 6 = 394
Q2. What will be remainder when (6767 + 67) is divided by 68 ?
Answer : Option C
Explaination / Solution:
(xn + 1) will be divisible by (x + 1) only when n is odd.
(6767 + 1) will be divisible by (67 + 1)
(6767 + 1) + 66, when divided by 68 will give 66 as remainder.
Q3. 
Directions: Study the table carefully to answer the questions that follow:
Candidates who appeared and passed in the test from four schools in six different years
What was the approximate percent increase in the number of candidates who passed in the exam from school-A in the year 2009 as compared to the previous year?
Answer : Option C
Explaination / Solution:
Number of passed candidates from school A in the year 2008 = 346
Number of passed candidates from school A in the year 2009 = 435
Percentage Increase = (89/346)*100
= 26 (approx)
Q4. What type of geometric drawing is shown below?
Answer : Option A
Explaination / Solution:
No Explaination.
Q5. For a job, a candidate must fulfill the following criteria:
The age should be from 24 to 30 as on 15th April 2017. Must have secured at least 58% marks in BSc – Math. Must have done post-graduate in Math or Statistics with at least 62% marks. Must have an experience of at least 2 years. Must have secured at least 60% in written test and 70% in interview.
Sahil fulfills all the following criteria, then which of the following criterion/criteria is not essential for final selection?
(i) He was born on 7th July 1988.
(ii) He completed his graduation with 66% marks and secured 76% marks in class 12.
(iii) He has worked for 3 years in ABC Company.
(iv) He got 72% in written test and 75% in interview.
(v) He did his graduation and post-graduation in Math.
(vi) He secured 64% marks in post-graduation.
The age should be from 24 to 30 as on 15th April 2017. Must have secured at least 58% marks in BSc – Math. Must have done post-graduate in Math or Statistics with at least 62% marks. Must have an experience of at least 2 years. Must have secured at least 60% in written test and 70% in interview.
Sahil fulfills all the following criteria, then which of the following criterion/criteria is not essential for final selection?
(i) He was born on 7th July 1988.
(ii) He completed his graduation with 66% marks and secured 76% marks in class 12.
(iii) He has worked for 3 years in ABC Company.
(iv) He got 72% in written test and 75% in interview.
(v) He did his graduation and post-graduation in Math.
(vi) He secured 64% marks in post-graduation.
Answer : Option E
Explaination / Solution:
According to the conditions, graduation must be BSc – Math. But in points (i) to (vi) – this is not specified anywhere.
Q6. The difference between simple and compound interests compounded annually on a certain sum of money for 2 years at 4% per annum is Re. 1. The sum (in Rs.) is:
Answer : Option A
Explaination / Solution:
Let the sum be Rs. x. Then,
| C.I. = |  | x |  | 1 + | 4 |  | 2 | - x |  | = | | 676 | x | - x | | = | 51 | x. |
| 100 | 625 | 625 |
| S.I. = | | x x 4 x 2 | | = | 2x | . |
| 100 | 25 |
| 51x | - | 2x | = 1 |
| 625 | 25 |
x = 625.
Q7.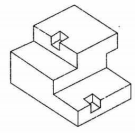 
Answer : Option B
Explaination / Solution:
No Explaination.
Q8. What is the value of m in the quadratic equation x2 + mx +24=0 if one of its roots is 
Answer : Option D
Explaination / Solution:
X =
3/2 in x2 +
mx + 24 = 0
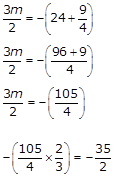
(3/2) + m*(3/2) + 24 = 0
(9/4) + (3m/2) + 24 = 0
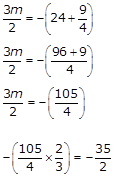
Q9. For which of the following companies the rise or fall in production of grocery goods from 2013 to 2014 was the maximum?
Answer : Option A
Explaination / Solution:
Company P, the rise in production of grocery goods from 2013 to 2014
= (35-25)/25 *100 = +40 %
Company Q, the fall in production of grocery goods from 2013 to 2014
= (45-15)/45 *100 = -66.66 %
Company R, the rise in production of grocery goods from 2013 to 2014
= (35-15)/15 *100 = +133.33 %
Company S, the rise in production of grocery goods from 2013 to 2014
= (35-20)/20 *100 = +75 %
Company T, the fall in production of grocery goods from 2013 to 2014
= (25-15)/25 *100 = -40 %
So, Maximum rise in company R
Q10. 'alibi' means a plea by an accused person that he -
Answer : Option B
Explaination / Solution:
No Explaination.
