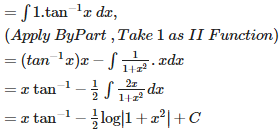CBSE 12TH MATHEMATICS - Online Test
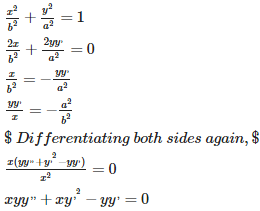
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below:
Food | Vitamin A | Vitamin B | Vitamin C |
X | 1 | 2 | 3 |
Y | 2 | 2 | 1 |
One kg of food X costs Rs 16 and one kg of food Y costs Rs 20. Find the least cost of the mixture which will produce the required diet?
Let number of kgs of food of brand X = x
And number of kgs. of food of brand Y = y
Therefore , the above L.P.P. is given as :
Minimise , Z = 16x +20y , subject to the constraints : x + 2y ≥ 10,2x + 2y ≥12,3x + y ≥8,x,y ≥ 0.,
Corner points | Z =16x +20 y |
C(10 , 0 ) | 160
|
B (0,8) | 160 |
D(1,5 ) | 116 |
A(2,4) | 112……………..(Min.) |
Here Z = 112 is minimum.
i.e. Least cost of the mixture is Rs 112 (2 kg of Food X and 4 kg of food Y).

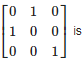

The area bounded by the curves and is equal to

Required area:

Domain of f(x) =
If A and B are square matrices of the same order, then implies