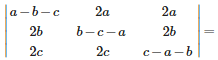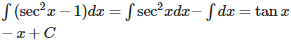CBSE 12TH MATHEMATICS - Online Test
Q1.
For the differential equationfind the solution curve passing through the point (1, –1).
Answer : Option D
Explaination / Solution:
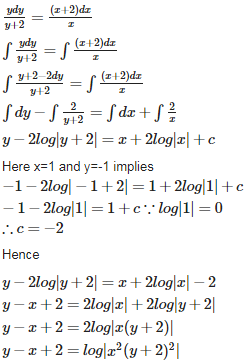
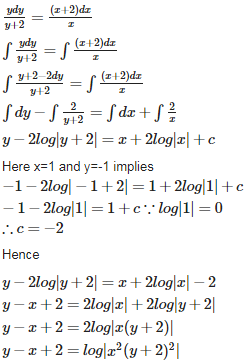
Q2. The equation of the tangent to the curve at the point (0, 1) is
Answer : Option B
Explaination / Solution:
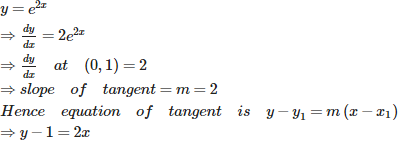
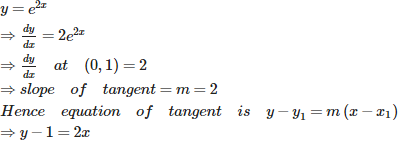
Q3. Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 11 units of vitamin B. Food P costs Rs 60/kg and Food Q costs Rs 80/kg. Food P contains 3 units/kg of Vitamin A and 5 units / kg of Vitamin B while food Q contains 4 units/kg of Vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.
Answer : Option B
Explaination / Solution:
Let number of food type P = x
And number of units of food type Q = y
Therefore , the above L.P.P. is given as :
Minimise , Z = 60x +80y , subject to the constraints : 3 x + 4y ≥ 8, 5x + 2y ≥ 11, x,y ≥ 0.
The corner points can be obtained by drawing the lines 3x+4y=8 and 5x+2y=11 graphically.
The points so obtained are (8/3,0), (2,1/2), (0,11/2)
Corner points | Z = - x + 2y |
D(8/3,0 ) | 160………………….(Min.) |
A(2,1/2) | 160………………(Min.) |
B(0,11/2) | 440 |
Here Z = 160 is minimum. i.e. Minimum cost = Rs 160 at all points lying on segment joining .
Q4.
The area bounded by the curves is given by
Answer : Option A
Explaination / Solution:
Both and are symmetric about y – axis and on solving them we get :
required area :
=
required area :
=
Q5. A relation R on a set A is called an empty relation if
Answer : Option C
Explaination / Solution:
For any set A ,an empty relation may be defined on A as: there is no element exists in the relation set which satisfies the relation for a given set A i.e.
let A={1,2,3,4,5} and R={(a,b): a,b ∈A and a+b= 10},so we get R={ } which is an empty relation.
Q8. Magnitude of the vector 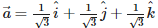 is
is
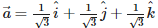 is
is
Answer : Option B
Explaination / Solution:
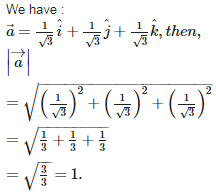
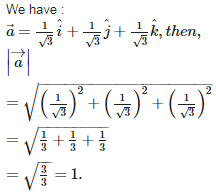
Q9. If , then the value of is
Answer : Option A
Explaination / Solution:


Q10. Let f and g be differentiable functions such that fog = I, the identity function. If g’ (a) = 2 and g (a) = b, then f ‘ (b) =
Answer : Option C
Explaination / Solution: