CBSE 11TH MATHEMATICS - Online Test

Answer : Option B
Explaination / Solution:

Let P(x,y) represent the complex number  Z=x+iy  in the complex plane(Argand plane) and let O(0,0) be the origin

Then we have OP=x2+y2−−−−−−√

Here Z=1+i so that P(x,y)=P(1,1)

Hence OP=1+1−−−−√=2–√

Answer : Option B
Explaination / Solution:

x2+1=0⇒x2=−1⇒x2=−1−−−√⇒x=i∈C

[i=imaginory root of unity which is a complex no.]

since the solution of x doesnot belongs to real no hence the set is null set

Answer : Option B
Explaination / Solution:

Answer : Option B
Explaination / Solution:

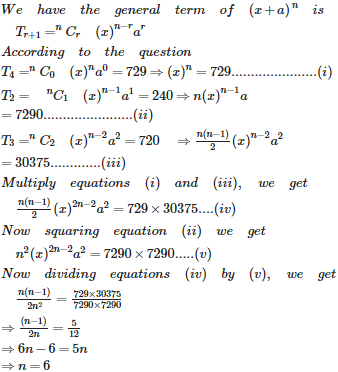
Let the length of the shortest piece be x cm.Then we have the length of the second and third pieces are x+3 and 2x centimeters respectively.

According to the question,

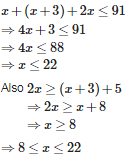
Hence the shortest piece may be atleast 8 cm long but it cannot be more than 22cm in length.

Answer : Option B
Explaination / Solution:

Ltx→0(sinx−xx3).(sinxx)=Ltx→0(sinx−xx3)

Now using L'Hospital we have, cosx−13x2

Again using L'Hospital, −sinx6x

Again using L'hospital; −16

Answer : Option C
Explaination / Solution:

Answer : Option B
Explaination / Solution:

H.M=31a+1b+1c=314+18+116=48/7=6.85

Answer : Option D
Explaination / Solution:

If the line is parallel to the given line x-2y + 5 =0,

then the required line will have same slope

Hence the equaion of the given line is x-2y+k=0

since it passes through the origin,

0+0+k=0

Therefore k=0

Hence the equation of the required line is x-2y=0 or x=2y

Answer : Option A
Explaination / Solution:

(∼p∧∼q)∨(∼p∧q)

∼p∧(∼q∨q) distributive law

∼p∧T    since ∼q∨q≡T

∼p  since ∼p∧T≡∼p

Answer : Option C
Explaination / Solution:

Since when n = 1 , we get the inequality as 1>1, which is not true. also for n = 2 , we get 2>2, which is false. Hence the given statement is true for n>2