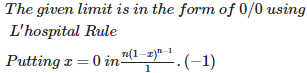CBSE 11TH MATHEMATICS - Online Test
Q1. Let A = { a,b,c } , B = { b,c,d } , C = { a,b,d,e } , then A∩(B∪C) is
Answer : Option B
Explaination / Solution:
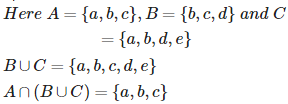
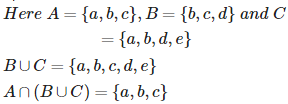
Q2. Let x,y∈R, then x + iy is a purely imaginary number if
Answer : Option B
Explaination / Solution:
Purely imaginary number is a complex number which has only imaginary part ( iy)
But if y=0 the complex number iy will become 0 which is real.
Hence the condition for a number to be purely imaginary is x=0 and
Q3. The term independent of x in the expansion of is
Answer : Option A
Explaination / Solution:


Q4. Identify solution set for | 4 − x | + 1 < 3?
Answer : Option A
Explaination / Solution:
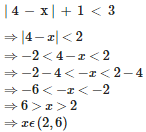
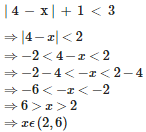
So solution set is ( 2 , 6 )
Q6. The eleventh term of the sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, ….. is
Answer : Option C
Explaination / Solution:
here,
Q7. If x and y are related as y – 4x = 3, then the nature of correlation between x and y is
Answer : Option C
Explaination / Solution:
comparinf the given equation with ax + by + c= 0
a = -4, b =1 and c= -3
so ab < 0
hence,
so a perfect positive correlation.
Q8. Slope of any line parallel to X axis is
Answer : Option B
Explaination / Solution:
Since the angle made with x axis is zero, since tanθ is the slope. Then tan0 = 0
Hence the slpoe of the line parallel to X-axis is zero
Q9. Let p and q be two prepositions given by p : To become an airforce officer one should be graduate. q : To become an airforce officer one should have good health. The compound proposition “ To become an airforce officer one should be a graduate and should have good health “ is represented by
Answer : Option A
Explaination / Solution:
the statement before and is p .The statement after and is q.and is replaced by∧
Q10. Let P ( n ) denote the statement is odd , It is seen that , therefore P ( n ) is true for all
Answer : Option A
Explaination / Solution:
Since if n = 1 the answer is 2 which is even . also p ( 1 ) = p ( 2 ) is also not true since p(2 ) is 6 which is even.